|
МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»
2006 год
Задачи для 5 класса
Лев записал в таблицу 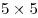 целые числа. Оказалось, что каждое число равно среднему арифметическому остальных 24 чисел. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно среднему арифметическому остальных 24 чисел. Могут ли в этой таблице быть различные числа?
Ник и Дик придумали себе игру. Сначала они выбирают три цифры (от 0 до 9; Ник — первую и третью, а Дик — вторую). Затем Дик выбирает арифметической действие (сложение, вычитание, умножение или деление). Ник должен поставить знак этого действия между двумя из выбранных цифр так, чтобы в итоге получилась третья (в любом порядке). Если он сумеет это сделать, то выигрывает, а если нет, то проиграл. Например, если названы цифры 1, 2, 3 и вычитание, то Ник выиграет (так как 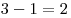 ), а если умножение, то проиграет. У которого из двух игроков есть возможность сделать беспроигрышный выбор? ), а если умножение, то проиграет. У которого из двух игроков есть возможность сделать беспроигрышный выбор?
Разбейте 2006 в сумму как можно большего числа различных натуральных слагаемых.
У Винни-Пуха есть несколько горшочков из-под меда и несколько лопнувших шариков. Так как красных шариков у Винни-Пуха было больше, чем шариков какого-либо другого цвета, то сначала он разложил в горшочки по одному красному шарику. Но несколько горшочков остались пустыми, и тогда Винни-Пух положил в них по одному зеленому шарику. Оставшиеся зеленые шарики он разложил в те горшочки, где уже лежали красные. Затем Винни-Пух разложил по горшочкам шарики остальных цветов, следя за тем, чтобы ни в одном горшочке не оказались два одинаковых шарика. Какое наименьшее число горшочков могло быть у Винни-Пуха?
Лев хочет раскрасить все точки плоскости в несколько цветов так, чтобы на каждой прямой отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Сколько календарных суток может занять промежуток времени из 2006 минут?
Задачи для 6 класса
Лев записал в таблицу 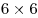 целые числа. Оказалось, что каждое число равно среднему арифметическому остальных 5 чисел своего столбца. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно среднему арифметическому остальных 5 чисел своего столбца. Могут ли в этой таблице быть различные числа?
Ник и Дик придумали себе игру. Сначала они выбирают три различные цифры (от 0 до 9; Ник — первую и третью, а Дик — вторую). Затем Дик выбирает арифметической действие (сложение, вычитание, умножение или деление). Ник должен поставить знак этого действия между двумя из выбранных цифр так, чтобы в итоге получилась третья (в любом порядке). Если он сумеет это сделать, то выигрывает, а если нет, то проиграл. Например, если выбраны цифры 1, 2, 3 и вычитание, то Ник выиграет (так как 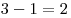 ), а если умножение, то проиграет. У которого из двух игроков есть возможность сделать беспроигрышный выбор? ), а если умножение, то проиграет. У которого из двух игроков есть возможность сделать беспроигрышный выбор?
У Винни-Пуха есть несколько горшочков из-под меда и несколько лопнувших шариков. Так как красных шариков у Винни-Пуха было больше, чем шариков какого-либо другого цвета, то сначала он разложил в горшочки по одному красному шарику. Но несколько горшочков остались пустыми, и тогда Винни-Пух положил в них по одному зеленому шарику. Оставшиеся зеленые шарики он разложил в те горшочки, где уже лежали красные. Затем Винни-Пух разложил по горшочкам шарики остальных цветов, следя за тем, чтобы в каждом горшочке оказалось разное число шариков. Какое наименьшее число горшочков могло быть у Винни-Пуха?
Лев утверждает, что если сумма цифр числа, записанного в системе счисления с основанием 2006, делится на 2005, то и само число тоже делится на 2005. Прав ли он?
Лев хочет раскрасить все точки плоскости в несколько цветов так, чтобы на каждой прямой отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Одну из сторон прямоугольника увеличили на 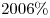 . На сколько процентов нужно уменьшить другую его сторону, чтобы площадь прямоугольника осталась прежней? . На сколько процентов нужно уменьшить другую его сторону, чтобы площадь прямоугольника осталась прежней?
Задачи для 7 класса
Лев записал в таблицу 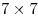 целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую сторону. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую сторону. Могут ли в этой таблице быть различные числа?
Ник утверждает, что если натуральное число делится на 2006, то при делении на 2005 оно даст в остатке 1. Прав ли Ник?
У Винни-Пуха есть несколько горшочков из-под меда и несколько лопнувших шариков. Так как красных шариков у Винни-Пуха было больше, чем шариков какого-либо другого цвета, то сначала он разложил в горшочки по одному красному шарику. Но несколько горшочков остались пустыми, и тогда Винни-Пух положил в них по одному зеленому шарику. Оставшиеся зеленые шарики он разложил в те горшочки, где уже лежали красные. Затем Винни-Пух разложил по горшочкам шарики остальных цветов, следя за тем, чтобы в каждом горшочке оказалось разное число шариков. Какое наименьшее число шариков могло быть у Винни-Пуха?
Найдите оба корня уравнения 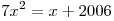 . .
Одну из сторон прямоугольника увеличили на 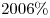 . На сколько процентов нужно уменьшить другую его сторону, чтобы площадь прямоугольника осталась прежней? . На сколько процентов нужно уменьшить другую его сторону, чтобы площадь прямоугольника осталась прежней?
Лев утверждает, что если сумма цифр числа, записанного в системе счисления с основанием 2006, делится на 5, то и само число тоже делится на 5. Прав ли он?
Задачи для 8 класса
Лев вписал целые числа в клетки шахматной доски (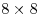 ). Оказалось, что каждое число на белой клетке равно среднему арифметическому остальных 7 чисел своего столбца, а каждое число на черной клетке равно среднему арифметическому остальных 7 чисел своей строки. Могут ли в этой таблице быть различные числа? ). Оказалось, что каждое число на белой клетке равно среднему арифметическому остальных 7 чисел своего столбца, а каждое число на черной клетке равно среднему арифметическому остальных 7 чисел своей строки. Могут ли в этой таблице быть различные числа?
Существует ли треугольник, площадь и длины двух сторон которого равны 2006?
Лев хочет раскрасить все точки плоскости в несколько цветов так, чтобы на каждой окружности отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Докажите, что 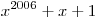 можно разложить в произведение двух многочленов (выше первой степени) с целыми коэффициентами. можно разложить в произведение двух многочленов (выше первой степени) с целыми коэффициентами.
У Винни-Пуха есть несколько горшочков из-под меда и несколько лопнувших шариков. Так как красных шариков у Винни-Пуха было больше, чем шариков какого-либо другого цвета, то сначала он разложил в горшочки по одному красному шарику. Но несколько горшочков остались пустыми, и тогда Винни-Пух положил в них по одному зеленому шарику. Оставшиеся зеленые шарики он разложил в те горшочки, где уже лежали красные. Затем Винни-Пух разложил по горшочкам шарики остальных цветов, следя за тем, чтобы во всех горшочках оказались разные комбинации шариков. Какое наименьшее число шариков могло быть у Винни-Пуха?
Лев утверждает, что если сумма цифр числа, записанного в системе счисления с основанием 2006, делится на 5, то и само число тоже делится на 5. Назовите еще два делителя с этим же свойством.
Задачи для 9 класса
Лев записал в таблицу 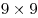 целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую вершину или сторону. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую вершину или сторону. Могут ли в этой таблице быть различные числа?
Разбейте 2006 в сумму как можно меньшего числа квадратов натуральных чисел.
Лев хочет раскрасить все точки плоскости в несколько цветов так, чтобы на каждой окружности отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Докажите, что 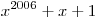 можно разложить в произведение двух многочленов (выше первой степени) с целыми коэффициентами. можно разложить в произведение двух многочленов (выше первой степени) с целыми коэффициентами.
Длины двух сторон треугольника зафиксированы, а третья может меняться. В каком случае радиус окружности, описанной вокруг такого треугольника, окажется минимально возможным?
Найдите все корни уравнения 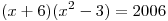 . .
Задачи для 10 класса
Лев записал в таблицу 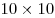 целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую вершину, но не имеющие с ней общей стороны. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую вершину, но не имеющие с ней общей стороны. Могут ли в этой таблице быть различные числа?
Существует ли ромб, площадь и длины каждой из сторон которого равны 2006?
Разбейте 2006 в сумму как можно меньшего числа кубов натуральных чисел.
Лев хочет раскрасить все точки плоскости в несколько цветов так, чтобы на каждой окружности отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Длины двух сторон треугольника зафиксированы, а третья может меняться. Чему она равна в случае, когда радиус окружности, описанной вокруг такого треугольника, становится минимально возможным?
Может ли иметь 2006-угольное сечение многогранник, у которого нет ни одного треугольного сечения?
Задачи для 11 класса
Лев записал в таблицу 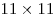 целые числа. Оказалось, что каждое число равно сумме чисел, записанных в клетки, имеющие с данной общую вершину или сторону. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно сумме чисел, записанных в клетки, имеющие с данной общую вершину или сторону. Могут ли в этой таблице быть различные числа?
Существует ли 2006-угольник, площадь и длины каждой из 2006 сторон которого равны 2006?
Лев хочет раскрасить все точки пространства в несколько цветов так, чтобы на каждой сфере отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Длины двух сторон треугольника зафиксированы, а третья может меняться. Чему равен минимально возможный радиус окружности, описанной вокруг такого треугольника?
Найдите наименьшее натуральное число 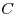 , для которого не существует таких натуральных чисел , для которого не существует таких натуральных чисел  и и  , что , что 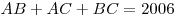 . .
Верно ли, что если 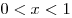 , то , то
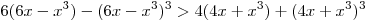 ? ?
Задачи для 12 класса
Лев записал в таблицу 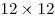 целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую вершину, но не имеющие с ней общей стороны. Могут ли в этой таблице быть различные числа? целые числа. Оказалось, что каждое число равно среднему арифметическому чисел, записанных в клетки, имеющие с данной общую вершину, но не имеющие с ней общей стороны. Могут ли в этой таблице быть различные числа?
Найдите наибольшее натуральное число 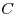 , для которого существуют такие натуральные числа , для которого существуют такие натуральные числа  и и  , что , что 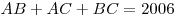 . .
Лев хочет раскрасить все точки пространства в несколько цветов так, чтобы на каждой сфере отсутствовали точки хотя бы одного из использованных им цветов. Какое наименьшее число цветов потребуется для такой раскраски?
Длины двух сторон треугольника зафиксированы, а третья может меняться. Чему равен минимально возможный радиус окружности, описанной вокруг такого треугольника?
На Новый год Льву подарили чудо-компьютер. Если в компьютер ввести функцию, то он вычисляет значение определенного интеграла от 2006-ой степени этой функции по промежутку от 0 до 10. Лев сначала ввел 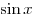 , а затем , а затем 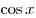 . Какое из двух выданных компьютером чисел больше и сколь велика разность между ними? . Какое из двух выданных компьютером чисел больше и сколь велика разность между ними?
Верно ли, что если 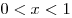 , то , то
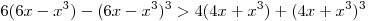 ? ?
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

