|
Единый государственный экзамен по математике, 2005 год
Часть A
A1. Внесите множитель под знак корня ![9\sqrt[7]{{q^3}} 9\sqrt[7]{{q^3}}](/inc/pictures/a51a6fd311ccfa6052949eb7ce56e58b.png) . .
A2. Найдите значение выражения 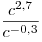 при при 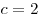 . .
A3. Найдите значение выражения 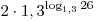 . .
A4. Упростите выражение 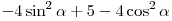 . .
A5. На одном из рисунков изображен график нечетной функции. Укажите этот рисунок.
A6. Найдите множество значений функции 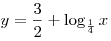 . .
A7. Решите неравенство 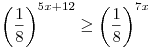 . .
A8. Решите неравенство 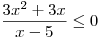 . .
A9. Решите уравнение 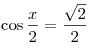 . .
A10. Найдите производную функции 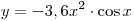 . .
Часть B
B1. Решите уравнение 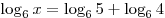 . .
B2. Решите уравнение 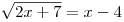 . .
B3. Найдите угловой коэффициент касательной к графику функции 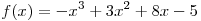 в точке с абсциссой в точке с абсциссой 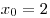 . .
B4. Вычислите: ![\sqrt[3]{{7 + 2\sqrt 6 }} \cdot \sqrt[3]{{2\sqrt 6 - 7}} \cdot \sqrt[3]{{40}} \sqrt[3]{{7 + 2\sqrt 6 }} \cdot \sqrt[3]{{2\sqrt 6 - 7}} \cdot \sqrt[3]{{40}}](/inc/pictures/9ba9d3b1157466a38356874676a36b7e.png) . .
B5. Найдите значение выражения 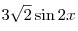 , если , если 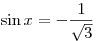 , , 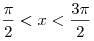 . .
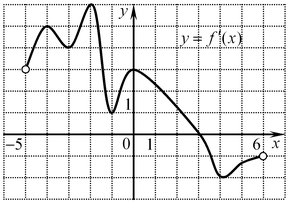 B6. Функция
B6. Функция  определена на промежутке определена на промежутке
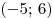 . На рисунке изображен график ее производной.
Найдите точку . На рисунке изображен график ее производной.
Найдите точку 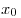 , в которой функция , в которой функция  принимает наибольшее значение.
принимает наибольшее значение.
B7. Найдите сумму всех корней уравнения 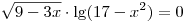 . .
B8. Найдите значение функции 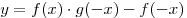 в точке в точке 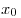 , если известно, что функция , если известно, что функция  четная, функция четная, функция 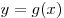 нечетная, нечетная,
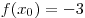 , , 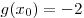 . .
B9. В бидон налили 4 литра молока трехпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов
составляет жирность молока в бидоне?
B10. Боковое ребро правильной четырехугольной призмы равно стороне ее основания. Расстояние между серединами непараллельных ребер, принадлежащих разным основаниям, равно 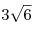 . Найдите объем призмы. . Найдите объем призмы.
B11. В равнобедренном треугольнике  с основанием с основанием 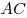 высоты высоты 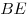 и и 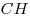 пересекаются в точке пересекаются в точке 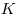 , причем , причем 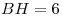 , , 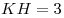 . Найдите площадь треугольника . Найдите площадь треугольника 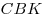 . .
Часть C
C1. Найдите все значения  , для которых точки графика функции , для которых точки графика функции 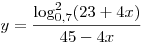 лежат выше соответствующих точек графика функции лежат выше соответствующих точек графика функции 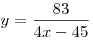 . .
C2. Решите уравнение 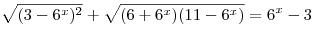 . .
C3. Найдите положительные значения  , при каждом из которых наименьшее из двух чисел , при каждом из которых наименьшее из двух чисел 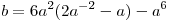 и и 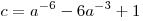 не меньше не меньше 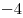 . .
C4. Через центр 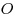 данной сферы проведено сечение. Точка данной сферы проведено сечение. Точка 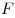 выбрана на сфере, а точки выбрана на сфере, а точки  , ,  , , 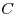 , , 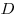 — последовательно на окружности сечения так, что объем пирамиды — последовательно на окружности сечения так, что объем пирамиды 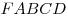 наибольший. Точки наибольший. Точки  , , 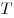 , , 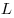 — середины ребер — середины ребер 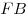 , , 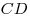 и и 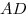 соответственно. Площадь треугольника соответственно. Площадь треугольника 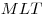 равна равна 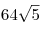 . Найдите радиус сферы. . Найдите радиус сферы.
C5. Даны два уравнения:
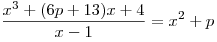 и
и
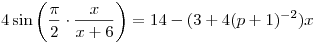 . .
Значение параметра  выбирается так, что выбирается так, что 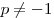 и при умножении числа различных корней первого уравнения на число различных корней второго уравнения получается число и при умножении числа различных корней первого уравнения на число различных корней второго уравнения получается число 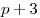 . Решите второе уравнение при каждом значении параметра, выбранном таким образом. . Решите второе уравнение при каждом значении параметра, выбранном таким образом.
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 4 |
2 |
3 |
1 |
4 |
3 |
2 |
4 |
1 |
1 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
B10 |
B11 |
 |
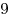 |
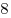 |
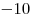 |
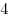 |
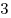 |
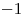 |
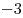 |
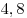 |
 |
 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
