|
Единый государственный экзамен по математике, 2006 год
Часть A
A1. Упростите выражение 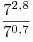 . .
Решение. Поскольку 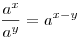 , получаем: , получаем:
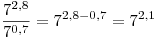 . .
Правильный ответ: 2.
A2. Найдите значение выражения 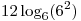 . .
Решение. Так как 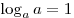 и и 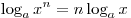 при при 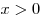 имеем: имеем:
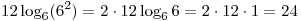 . .
Правильный ответ: 3.
A3. Вычислите ![\sqrt[3] {125 \cdot 0,027} \sqrt[3] {125 \cdot 0,027}](/inc/pictures/3ea8ff9105b7cb6ee7604175c2c712d7.png) . .
Решение. Используя формулы ![\sqrt[n] {ab} = \sqrt[n]{a} \cdot \sqrt[n]{b} \sqrt[n] {ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}](/inc/pictures/6b0090f96005c2bcd44f623b1cee8393.png) и и ![\sqrt[n]{a^n} = a \sqrt[n]{a^n} = a](/inc/pictures/e641c095268b996e48151945f81141d5.png) ( (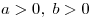 ), получаем: ), получаем:
![\sqrt[3]{{125 \cdot 0,027}} = \sqrt[3]{{125}} \cdot
\sqrt[3]{{0,027}} = \sqrt[3]{{5^3 }} \cdot \sqrt[3]{{0,3^3 }} = 5 \cdot
0,3 = 1,5 \sqrt[3]{{125 \cdot 0,027}} = \sqrt[3]{{125}} \cdot
\sqrt[3]{{0,027}} = \sqrt[3]{{5^3 }} \cdot \sqrt[3]{{0,3^3 }} = 5 \cdot
0,3 = 1,5](/inc/pictures/ea38499aaa28c3268870a8bd774c541d.png) . .
Правильный ответ: 1.
A4. На каком из следующих рисунков изображен график функции, возрастающий на промежутке ![[ - 1;\;2] [ - 1;\;2]](/inc/pictures/0e1d98058f782a0dba4b3874f6bfa8b9.png) ? ?
Решение. Функция возрастает на промежутке, если для любых двух значении аргумента из этого промежутка большему из них соответствует большее значение функции.
Правильный ответ: 4.
A5. Найдите множество значений функции 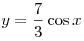 . .
Решение. Так как 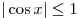 , имеем: , имеем:
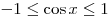 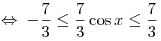 . .
Правильный ответ: 2.
A6. Найдите область определения функции ![f(x) = \frac{{31}}{{4 - \sqrt[4]{x}}} f(x) = \frac{{31}}{{4 - \sqrt[4]{x}}}](/inc/pictures/198f72178cffd22b0671eb6b831c0896.png) . .
Решение. Область определения данной функции задается системой ![\left\{ \begin{array}{l} x \ge 0, \\ 4 - \sqrt[4]{x} \ne 0. \\\end{array} \right. \left\{ \begin{array}{l} x \ge 0, \\ 4 - \sqrt[4]{x} \ne 0. \\\end{array} \right.](/inc/pictures/8528f57fb2906279bf42056836621151.png)
Имеем:
![\left\{ \begin{array}{l} x \ge 0, \\ 4 - \sqrt[4]{x} \ne 0. \\\end{array} \right. \left\{ \begin{array}{l} x \ge 0, \\ 4 - \sqrt[4]{x} \ne 0. \\\end{array} \right.](/inc/pictures/8528f57fb2906279bf42056836621151.png) ![\; \Leftrightarrow \;\left\{\begin{array}{l} x \ge 0, \\\sqrt[4]{x} \ne 4 \\\end{array} \right.\; \Leftrightarrow \;\left\{ \begin{array}{l}x \ge 0, \\x \ne 256 \\\end{array} \right.\; \Leftrightarrow \;\left[ \begin{array}{l}0 \le x < 256, \\256 < x < + \infty. \\\end{array} \right. \; \Leftrightarrow \;\left\{\begin{array}{l} x \ge 0, \\\sqrt[4]{x} \ne 4 \\\end{array} \right.\; \Leftrightarrow \;\left\{ \begin{array}{l}x \ge 0, \\x \ne 256 \\\end{array} \right.\; \Leftrightarrow \;\left[ \begin{array}{l}0 \le x < 256, \\256 < x < + \infty. \\\end{array} \right.](/inc/pictures/89f4f37134b49bc8b1fbbc8c743d538a.png)
Правильный ответ: 1.
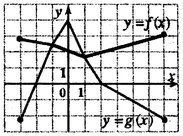 A7. На рисунке изображены графики функций
A7. На рисунке изображены графики функций  и и
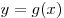 , заданных на промежутке , заданных на промежутке 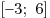 . Укажите
те значения . Укажите
те значения  , для которых выполняется неравенство , для которых выполняется неравенство 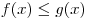 . .
Решение. Для решения задачи достаточно указать абсциссы всех тех точек графика функции  , которые лежат не выше точек графика функции , которые лежат не выше точек графика функции 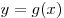 . .
Правильный ответ: 1.
A8. Найдите производную функции 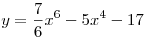 . .
Решение. Пользуясь формулой 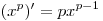 и правилами дифференцирования, получаем: и правилами дифференцирования, получаем:
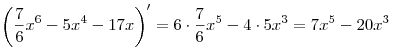 . .
Правильный ответ: 1.
A9. Решите уравнение 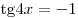 . .
Решение.
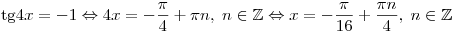 . .
Правильный ответ: 3.
A10. Решите неравенство 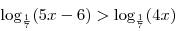 . .
Решение. Пользуясь свойствами логарифмической функции, основание которой меньше 1, имеем:
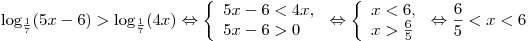 . .
Правильный ответ: 2.
Часть B
B1. Решите уравнение 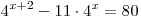 . .
Решение. Поскольку 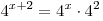 , вынося за скобки общий множитель , вынося за скобки общий множитель 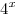 , получаем: , получаем:
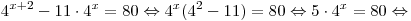
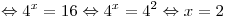 . .
Ответ: 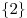 . .
B2. Решите уравнение 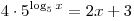 . .
Решение. Пользуясь основным логарифмическим тождеством и
учитывая условие существования логарифма, имеем:
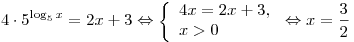 . .
Ответ: 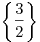 . .
B3. Найдите значение выражения 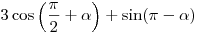 , если , если
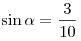 . .
Решение. Пользуясь формулами приведения, получаем:
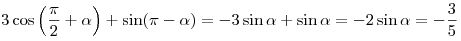 . .
Ответ: 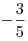 . .
B4. Вычислите: ![7\log _{9\sqrt[3]{3}}
(27\sqrt[3]{3}) 7\log _{9\sqrt[3]{3}}
(27\sqrt[3]{3})](/inc/pictures/3009f644b36a4c4dc13156161584a8e9.png) . .
Решение. Последовательно используем свойства степеней и логарифмов:
![7\log _{9\sqrt[3]{3}} (27\sqrt[3]{3}) = 7\log _{3^2 \cdot
3^{\frac{1}{3}} } (3^3 \cdot 3^{\frac{1}{3}} ) = 7\log_{3^{\frac{7}{3}} } (3^{\frac{{10}}{3}} ) = 7 \cdot \frac{3}{7} \cdot
\frac{{10}}{3}\log _3 3 = 10 7\log _{9\sqrt[3]{3}} (27\sqrt[3]{3}) = 7\log _{3^2 \cdot
3^{\frac{1}{3}} } (3^3 \cdot 3^{\frac{1}{3}} ) = 7\log_{3^{\frac{7}{3}} } (3^{\frac{{10}}{3}} ) = 7 \cdot \frac{3}{7} \cdot
\frac{{10}}{3}\log _3 3 = 10](/inc/pictures/36c7c0cd9f3511e80f3a9675a951d97b.png) . .
Ответ: 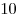 . .
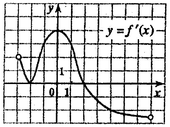 B5. К графику функции
B5. К графику функции  в точке с абсциссой в точке с абсциссой 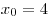 проведена касательная. Найдите ее угловой
коэффициент, если на рисунке изображен график производной этой функции. проведена касательная. Найдите ее угловой
коэффициент, если на рисунке изображен график производной этой функции.
Решение. Угловой коэффициент касательной к графику функции
 в точке с абсциссой в точке с абсциссой 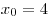 равен
значению производной функции равен
значению производной функции  в этой точке, т.е. в этой точке, т.е.
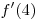 . .
Ответ: 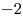 . .
B6. Найдите разность между наибольшим и наименьшим значениями функции 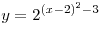 на отрезке на отрезке 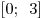 . .
Решение. Парабола 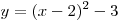 , ветви которой
направлены вверх, имеет вершину в точке , ветви которой
направлены вверх, имеет вершину в точке 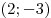 , следовательно, функция , следовательно, функция 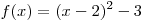 убывает на
отрезке убывает на
отрезке ![[0;\,2] [0;\,2]](/inc/pictures/fc0441ee3fa76e443cde8129362cf539.png) и возрастает на отрезке и возрастает на отрезке ![[2;\,3] [2;\,3]](/inc/pictures/63233589fd1233e364bdb3a99af55d5b.png) . Имеем: . Имеем: 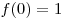 , , 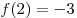 , , 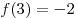 .
Показательная функция с основанием, большим .
Показательная функция с основанием, большим 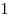 , – функция
возрастающая, откуда , – функция
возрастающая, откуда ![\mathop {\max }\limits_{[0;\;3]} (2^{f(x)} )
= 2^1 = 2 \mathop {\max }\limits_{[0;\;3]} (2^{f(x)} )
= 2^1 = 2](/inc/pictures/5233e52a31d5f92137f13bbcca4403b5.png) , , ![\mathop {\min }\limits_{[0;\;3]} (2^{f(x)} ) = 2^{ - 3} = \frac{1}{8} = 0,125 \mathop {\min }\limits_{[0;\;3]} (2^{f(x)} ) = 2^{ - 3} = \frac{1}{8} = 0,125](/inc/pictures/7e5072a9617da3f82604d6ef2f97ab65.png) . .
Искомая разность равна 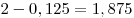 . .
Ответ: 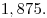
B7. Решите уравнение 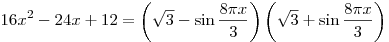 . .
Решение.
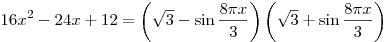
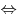 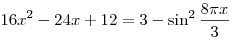 . .
Парабола 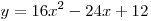 , ветви которой направлены вверх, имеет вершину в точке , ветви которой направлены вверх, имеет вершину в точке 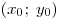 , где , где 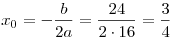 , , 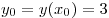 . Следовательно, . Следовательно, 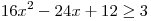 . .
С другой стороны, имеем 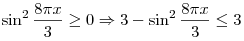 . .
Таким образом, данное уравнение равносильно системе 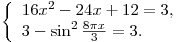
Единственное решение первого уравнения системы, 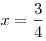 , удовлетворяет второму уравнению. Следовательно, это решение системы. , удовлетворяет второму уравнению. Следовательно, это решение системы.
Ответ: 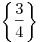 . .
B8. Найдите значение функции 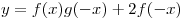 в точке в точке 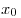 , если известно, что функция , если известно, что функция  – четная, функция – четная, функция 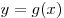 – нечетная, – нечетная, 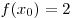 , , 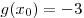 . .
Решение. По условию, функция  – четная, а функция – четная, а функция 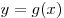 – нечетная, следовательно, – нечетная, следовательно, 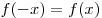 , , 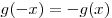 . Тогда данная функция . Тогда данная функция 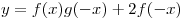 принимает вид принимает вид 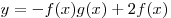 , откуда находим: , откуда находим: 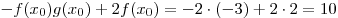 . .
Ответ: 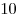 . .
B9. Объемы ежегодной добычи нефти первой, второй и третьей скважинами относятся как 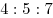 . Планируется уменьшить годовую добычу нефти из первой скважины на . Планируется уменьшить годовую добычу нефти из первой скважины на 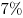 и из второй – тоже на и из второй – тоже на 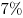 . На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился? . На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?
Решение. Примем объем ежегодной добычи нефти из первой скважины за 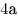 , тогда объемы ежегодной добычи нефти второй и третьей скважинами равны соответственно , тогда объемы ежегодной добычи нефти второй и третьей скважинами равны соответственно 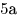 и и 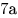 , а суммарный объем ежегодной добычи нефти равен , а суммарный объем ежегодной добычи нефти равен 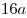 . После уменьшения годовой добычи нефти из первой и второй скважин на . После уменьшения годовой добычи нефти из первой и второй скважин на 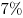 объем добываемой из них нефти будет равен объем добываемой из них нефти будет равен 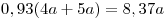 и на «долю» третьей скважины останется и на «долю» третьей скважины останется 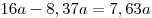 . Пусть . Пусть  – то количество процентов, на которое нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился. Тогда имеем – то количество процентов, на которое нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился. Тогда имеем 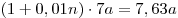 , откуда , откуда 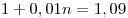 и, окончательно, и, окончательно, 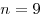 . .
Ответ: 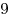 . .
B10. Основание прямой призмы 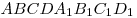 — параллелограмм — параллелограмм 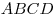 , в котором , в котором 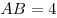 , , 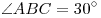 . Высота призмы равна 3. Найдите
тангенс угла между плоскостью основания призмы и плоскостью . Высота призмы равна 3. Найдите
тангенс угла между плоскостью основания призмы и плоскостью 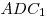 . .
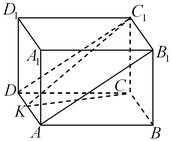 Решение. Построим высоту
Решение. Построим высоту 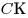 параллелограмм параллелограмм 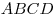 и соединим отрезком точки и соединим отрезком точки 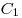 и и 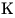 . (см. рис.). Поскольку . (см. рис.). Поскольку 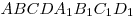 – прямая призма, – прямая призма, 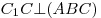 . Значит . Значит 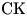 – проекция наклонной – проекция наклонной 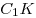 на плоскость на плоскость 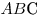 , и, на основании теоремы о трех перпендикулярах, , и, на основании теоремы о трех перпендикулярах, 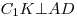 . Следовательно, угол . Следовательно, угол 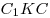 – линейный угол двугранного угла – линейный угол двугранного угла 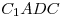 . Основание данной призмы – параллелограмм . Основание данной призмы – параллелограмм 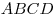 , откуда, на основании свойств параллелограмма, , откуда, на основании свойств параллелограмма, 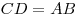 , , 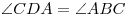 . .
Далее находим:
а) из прямоугольного треугольника 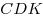 : : 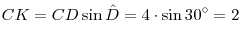 ; ;
б) из прямоугольного треугольника 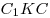 : : 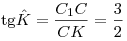 . .
Ответ:  . .
B11. Найдите площадь равнобедренной трапеции, если ее высота равна 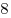 , а синус угла между диагональю и основанием равен , а синус угла между диагональю и основанием равен 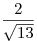 . .
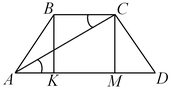 Решение. Пусть
Решение. Пусть 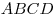 – данная трапеция ( – данная трапеция (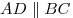 ), отрезки ), отрезки 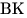 и и 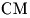 – ее высоты (см. рис). Поскольку – ее высоты (см. рис). Поскольку 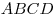 – равнобедренная трапеция, – равнобедренная трапеция, 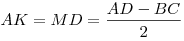 , откуда , откуда 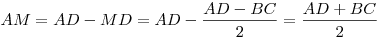 . Таким образом, отрезок . Таким образом, отрезок 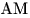 равен средней линии трапеции и, следовательно, равен средней линии трапеции и, следовательно, 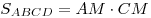 . .
Из прямоугольного треугольника 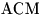 находим: находим:
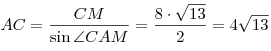 ; ; 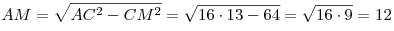 . .
Окончательно имеем 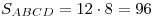 . .
Ответ: 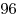 . .
Часть C
C1. Решите уравнение 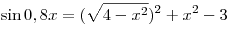 . .
Решение. Область допустимых значений (ОДЗ) задается неравенством 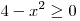 , решая которое, получаем , решая которое, получаем 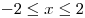 . На этом множестве имеем . На этом множестве имеем
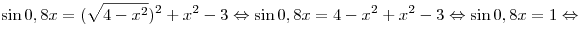
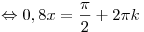 , , 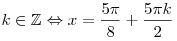 , , 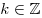 . .
Далее имеем:
а) если 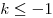 , то , то 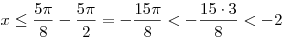 ; ;
б) если 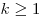 , то , то 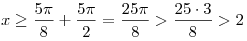 ; ;
в) если 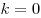 , то , то 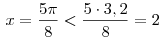 . .
Таким образом, 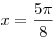 – единственный
корень данного уравнения. – единственный
корень данного уравнения.
Ответ: 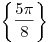 . .
С2. Найдите все значения  , при каждом из которых расстояние между соответствующими точками графиков функций , при каждом из которых расстояние между соответствующими точками графиков функций 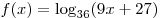 и и 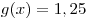 меньше, чем 0,25. меньше, чем 0,25.
Решение. Искомое множество совпадает с множеством решений неравенства 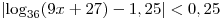 . .
Решим это неравенство:
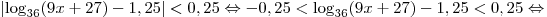
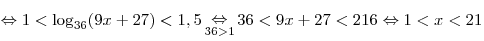 . .
Ответ: 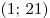 . .
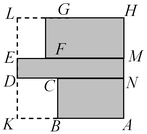 С3. Требуется разметить на земле участок
С3. Требуется разметить на земле участок 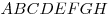 площадью 2000 м2, состоящий из трех прямоугольных частей и имеющий форму, изображенную на рисунке, где площадью 2000 м2, состоящий из трех прямоугольных частей и имеющий форму, изображенную на рисунке, где 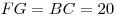 , , 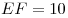 и и 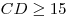 . Найдите
наименьшее значение периметра такого участка и какие-либо значения длин . Найдите
наименьшее значение периметра такого участка и какие-либо значения длин
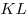 , , 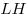 и и 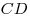 , при которых периметр является наименьшим. , при которых периметр является наименьшим.
Решение. Обозначим через  , , 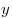 и и  соответственно длины отрезков
соответственно длины отрезков 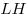 , , 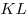 и площадь участка и площадь участка 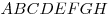 . Тогда периметр . Тогда периметр 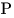 данного участка выражается формулой данного участка выражается формулой 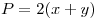 . .
О ценим площадь прямоугольника 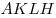 : :
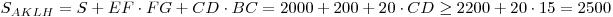 . .
Значит, 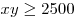 , откуда, учитывая , откуда, учитывая 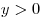 , получаем , получаем 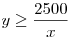 . Следовательно, . Следовательно, 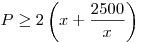 . .
Найдем наименьшее значение функции 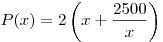 на промежутке на промежутке 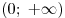 . (Учитывая условие, можно более точно указать интересующий нас промежуток: . (Учитывая условие, можно более точно указать интересующий нас промежуток: 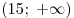 .) .)
На основании теоремы о среднем арифметическом и среднем геометрическом двух неотрицательных чисел получаем 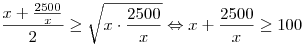 . При этом равенство достигается, тогда и только тогда, когда . При этом равенство достигается, тогда и только тогда, когда 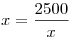 , откуда, учитывая , откуда, учитывая 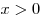 , получаем , получаем 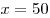 . (Исследование функции . (Исследование функции 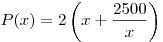 можно было также провести с помощью производной.) можно было также провести с помощью производной.)
Таким образом, 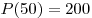 – наименьшее значение функции – наименьшее значение функции 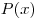 на промежутке на промежутке 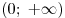 , и достигается оно при , и достигается оно при 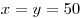 . При этом . При этом 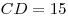 . .
Ответ: 200 м, 50 м, 50 м, 15 м.
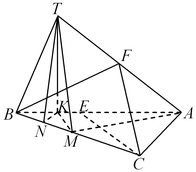 C4. В пирамиде
C4. В пирамиде 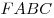 грани грани 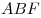 и и  перпендикулярны, перпендикулярны, 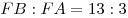 . Тангенс угла между прямой . Тангенс угла между прямой  и плоскостью и плоскостью 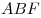 равен равен 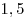 . Точка . Точка  выбрана на ребре выбрана на ребре  так, что так, что 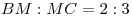 . Точка . Точка 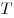 лежит на прямой лежит на прямой 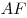 и равноудалена от точек и равноудалена от точек  и и  . Центр сферы, описанной около пирамиды . Центр сферы, описанной около пирамиды 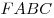 , лежит на ребре , лежит на ребре  , площадь этой сферы равна , площадь этой сферы равна 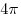 . Найдите объем пирамиды . Найдите объем пирамиды 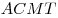 . .
Решение. Опустим перпендикуляры 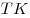 и и 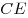 из точек из точек 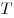 и и 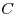 соответственно на плоскости соответственно на плоскости  и и 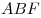 и перпендикуляр и перпендикуляр 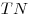 из точки из точки 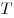 на прямую на прямую  , а также построим отрезки , а также построим отрезки 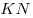 и и 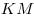 (см. рис). (см. рис).
Поскольку плоскости 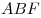 и и  перпендикулярны, точки перпендикулярны, точки 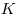 и и 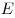 лежат на их линии пересечения – прямой лежат на их линии пересечения – прямой  и отрезки и отрезки 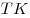 и и 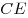 перпендикулярны перпендикулярны  . Кроме того, на основании теоремы о трех перпендикулярах, . Кроме того, на основании теоремы о трех перпендикулярах, 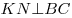 , так как , так как 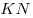 – проекция – проекция 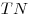 на плоскость на плоскость  . .
Отрезки 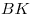 и и 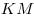 – проекции равных наклонных – проекции равных наклонных 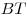 и и 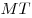 на плоскость на плоскость  , следовательно, , следовательно, 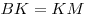 . Таким образом, отрезок . Таким образом, отрезок 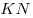 является высотой равнобедренного треугольника является высотой равнобедренного треугольника 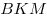 , а, следовательно, является и его медианой, откуда , а, следовательно, является и его медианой, откуда 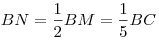 . .
Центр сферы, описанной около пирамиды 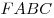 , лежит на ребре , лежит на ребре  , следовательно, , следовательно,  – диаметр – диаметр 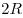 этой сферы. Так как любое сечение сферы плоскостью есть окружность, углы этой сферы. Так как любое сечение сферы плоскостью есть окружность, углы 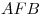 и и 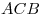 – вписанные углы, опирающиеся на диаметр – вписанные углы, опирающиеся на диаметр  , следовательно, , следовательно, 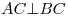 и и 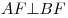 . .
Так как 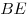 – проекция – проекция  на плоскость на плоскость 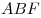 , угол , угол 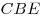 является углом между прямой является углом между прямой  и плоскостью и плоскостью 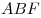 . .
Далее имеем:
1) По условию, площадь сферы, описанной около пирамиды 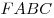 , равна , равна 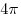 , откуда , откуда 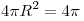 , , 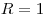 , , 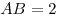 . .
2) Прямые 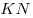 и и 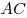 параллельны, так как они лежат в одной плоскости и перпендикулярны одной прямой параллельны, так как они лежат в одной плоскости и перпендикулярны одной прямой  , следовательно, , следовательно, 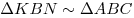 , откуда , откуда 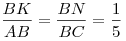 , , 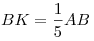 , а, значит, , а, значит, 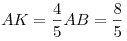 . .
3) В прямоугольном треугольнике  тангенс угла тангенс угла  равен равен 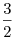 , следовательно, , следовательно, 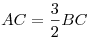 . Тогда . Тогда 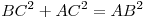 , , 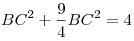 , , 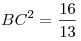 , , 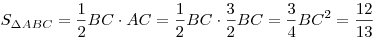 . .
4) Треугольники  и и 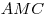 имеют общую высоту,
проведенную из вершены имеют общую высоту,
проведенную из вершены  , следовательно, отношение их площадей
равно отношению оснований , следовательно, отношение их площадей
равно отношению оснований 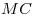 и и  , откуда получаем , откуда получаем 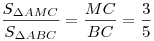 , , 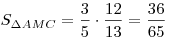 . .
5) Прямоугольные треугольники 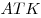 и и 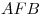 подобны, так как имеют общий острый угол подобны, так как имеют общий острый угол  , следовательно, , следовательно, 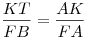 , откуда , откуда 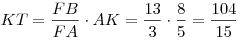 . .
Окончательно имеем
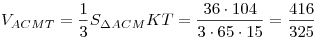 . .
Ответ: 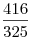 . .
C5. Найдите все значения  , при каждом из которых оба числа , при каждом из которых оба числа 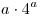 и и 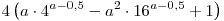 являются решениями
неравенства являются решениями
неравенства 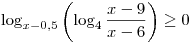 . .
Решение. Пусть 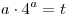 . Тогда . Тогда
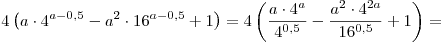
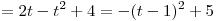 . .
Решим теперь неравенство 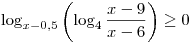 . .
1) Если 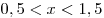 , то данное неравенство равносильно
системе неравенств , то данное неравенство равносильно
системе неравенств 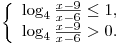
Решая эту систему, последовательно получаем:
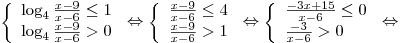
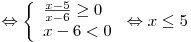 . .
Таким образом, все числа промежутка 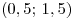 являются решениями данного неравенства. являются решениями данного неравенства.
2) Если 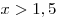 , то данное неравенство равносильно
неравенству , то данное неравенство равносильно
неравенству 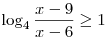 , решая
которое, получаем: , решая
которое, получаем:
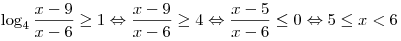 . .
Так как все числа промежутка 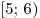 удовлетворяют условию удовлетворяют условию 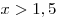 , они являются решениями данного неравенства. , они являются решениями данного неравенства.
Итак, множество 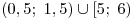 – есть множество решений данного неравенства и, по условию, числа – есть множество решений данного неравенства и, по условию, числа 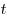 и и 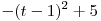 должны принадлежать этому множеству. должны принадлежать этому множеству.
Точка 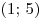 – вершина параболы – вершина параболы 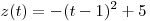 , ветви которой направлены вниз. , ветви которой направлены вниз.
На промежутке 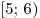 функция функция 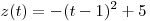 убывает и, если убывает и, если 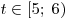 , то , то 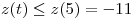 , т.е. в этом случае число , т.е. в этом случае число 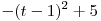 не является решением данного неравенства. не является решением данного неравенства.
Если 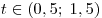 , то , то 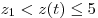 , где , где 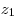 – меньшее из чисел – меньшее из чисел 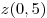 и и 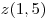 . Поскольку . Поскольку 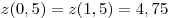 , в этом случае только число , в этом случае только число 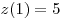 является решением данного неравенства. является решением данного неравенства.
Итак, только при 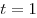 оба числа являются решениями данного неравенства. оба числа являются решениями данного неравенства.
Осталось решить относительно  уравнение уравнение 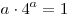 . (1) . (1)
При 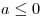 левая часть уравнения (1) неположительна, а правая положительна, значит, уравнение не имеет неположительных корней. левая часть уравнения (1) неположительна, а правая положительна, значит, уравнение не имеет неположительных корней.
При 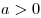 уравнение (1) равносильно уравнению уравнение (1) равносильно уравнению 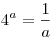 . (2) . (2)
Поскольку 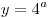 – возрастающая функция, а функция – возрастающая функция, а функция 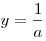 убывает при убывает при 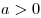 , уравнение (2) имеет на промежутке , уравнение (2) имеет на промежутке 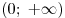 не более одного корня. Подбором находим не более одного корня. Подбором находим 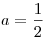 . .
Ответ: 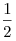 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

