|
Единый государственный экзамен по математике, 2007 год
Часть A
A1. Упростите выражение 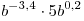 . .
Решение.
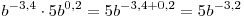 . .
Правильный ответ: 3.
A2. Вычислите: ![\frac{{\sqrt[3]{{189}}}}{{3\sqrt[3]{7}}} \frac{{\sqrt[3]{{189}}}}{{3\sqrt[3]{7}}}](/inc/pictures/7a6d08639255a96e3efb0391abe07ba5.png) . .
Решение.
![\frac{{\sqrt[3]{{189}}}}{{3\sqrt[3]{7}}} = \frac{{\sqrt[3]{{7 \cdot 27}}}}{{3\sqrt[3]{7}}} = \frac{{\sqrt[3]{7} \cdot \sqrt[3] {{27}}}}{{3\sqrt[3]{7}}} = \frac{{3\sqrt[3]{7}}}{{3\sqrt[3]{7}}} = 1 \frac{{\sqrt[3]{{189}}}}{{3\sqrt[3]{7}}} = \frac{{\sqrt[3]{{7 \cdot 27}}}}{{3\sqrt[3]{7}}} = \frac{{\sqrt[3]{7} \cdot \sqrt[3] {{27}}}}{{3\sqrt[3]{7}}} = \frac{{3\sqrt[3]{7}}}{{3\sqrt[3]{7}}} = 1](/inc/pictures/bb1ed97d6ce0a8b0f3e1cf99443dad9c.png) . .
Правильный ответ: 1.
A3. Найдите значение выражения 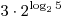 . .
Решение.
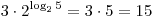 . .
Правильный ответ: 4.
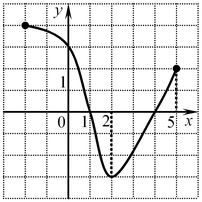
A4. Функция задана графиком. На каком из указанных промежутков она возрастает?
Решение: только на промежутке ![[2;\,5] [2;\,5]](/inc/pictures/2b8a0aa23b01531486a0fee31a8a9165.png) для любых для любых 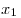 и и 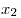 из этого промежутка выполняется
условие из этого промежутка выполняется
условие
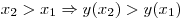 . .
Правильный ответ: 2.
A5. Найдите производную функции 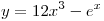 . .
Решение.
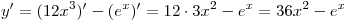 . .
Правильный ответ: 4.
A6. Найдите множество значений функции 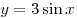 . .
Решение.
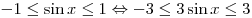 . .
Правильный ответ: 1.
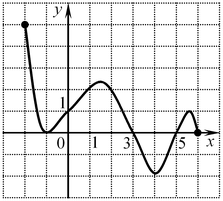
A7. Функция задана графиком. Укажите промежуток, на котором она принимает только отрицательные значения.
Решение: только на промежутке  все точки графика расположены ниже оси абсцисс. все точки графика расположены ниже оси абсцисс.
Правильный ответ: 2.
A8. Решите неравенство 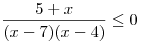 . .
Решение. Решим данное неравенство методом интервалов (см. рис.):

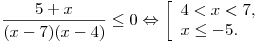
Правильный ответ: 4.
A9. Решите уравнение 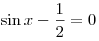 . .
Решение.
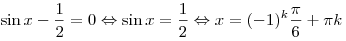 , , 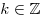 . .
Правильный ответ: 3.
A10. Решите неравенство 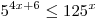 . .
Решение.
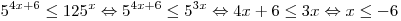 . .
Правильный ответ: 1.
Часть B
B1. Найдите значение выражения 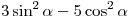 , если , если 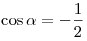 . .
Решение.
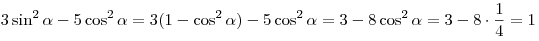 . .
Ответ: 1.
B2. Решите уравнение 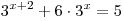 . .
Решение.
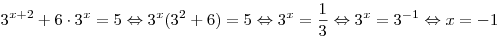 . .
Ответ: 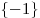 . .
B3. Решите уравнение 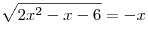 . .
Решение.
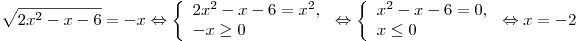 . .
Ответ: 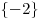 . .
B4. Найдите значение выражения 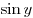 , если известно, что , если известно, что 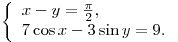
Решение.
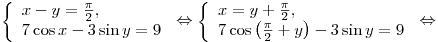
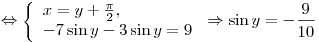 . .
Ответ: 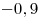 . .
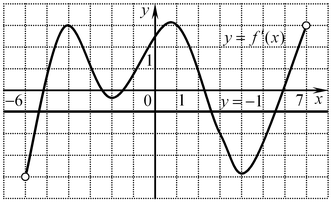 B5. Функция
B5. Функция  определена на промежутке определена на промежутке 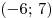 . На рисунке изображен график производной этой функции. К графику функции провели все касательные, параллельные прямой . На рисунке изображен график производной этой функции. К графику функции провели все касательные, параллельные прямой 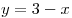 (или совпадающие с ней). Укажите количество точек графика функции, в которых проведены эти касательные. (или совпадающие с ней). Укажите количество точек графика функции, в которых проведены эти касательные.
Решение. Угловой коэффициент всех касательных, параллельных прямой 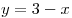 (или совпадающих с ней) равен (или совпадающих с ней) равен 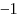 . С другой стороны, угловой коэффициент касательной к графику функции равен значению производной этой функции в точке касания. Нетрудно видеть, что производная, график которой изображен на рисунке, принимает значение . С другой стороны, угловой коэффициент касательной к графику функции равен значению производной этой функции в точке касания. Нетрудно видеть, что производная, график которой изображен на рисунке, принимает значение 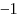 ровно в трех точках. ровно в трех точках.
Ответ: 3.
B6. Найдите значение выражения ![\sqrt[4] {(37 - 20\sqrt 3 )^2 }} + 2\sqrt 3 \sqrt[4] {(37 - 20\sqrt 3 )^2 }} + 2\sqrt 3](/inc/pictures/899998939213ab5a9194f8eaf5f2baae.png) . .
Решение:
а) преобразуем выражение ![\sqrt[4]{{(37 - 20\sqrt 3 )^2 }} \sqrt[4]{{(37 - 20\sqrt 3 )^2 }}](/inc/pictures/b197d8cc1de817abefe0c5ee441502ec.png) : :
![\sqrt[4]{{(37 - 20\sqrt 3 )^2 }} = \sqrt[4]{{(25 - 2 \cdot 5 \cdot 2\sqrt 3 + 12)^2 }} = \sqrt[4]{{(5^2 - 2 \cdot 5 \cdot 2\sqrt 3 + (2\sqrt 3 )^2 )^2 }} = \sqrt[4]{{(37 - 20\sqrt 3 )^2 }} = \sqrt[4]{{(25 - 2 \cdot 5 \cdot 2\sqrt 3 + 12)^2 }} = \sqrt[4]{{(5^2 - 2 \cdot 5 \cdot 2\sqrt 3 + (2\sqrt 3 )^2 )^2 }} =](/inc/pictures/3c475f8e625524fe234250f3f5e64680.png)
![= \sqrt[4]{{(5 - 2\sqrt 3 )^4 }} = |5 - 2\sqrt 3 | = \sqrt[4]{{(5 - 2\sqrt 3 )^4 }} = |5 - 2\sqrt 3 |](/inc/pictures/aca3cb8db1a691596ac70b080f71a144.png) ; ;
б) раскроем модуль: 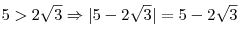 ; ;
в) выполним сложение: 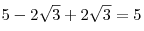 . .
Ответ: 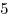 . .
B7. Решите уравнение ![\log _7 (3x + 5) +
\sqrt[4]{{\log _7^4 (2x + 5)}} = 0 \log _7 (3x + 5) +
\sqrt[4]{{\log _7^4 (2x + 5)}} = 0](/inc/pictures/e2148cf6855d401a06e8989f93880514.png) . (Если уравнение имеет более
одного корня, то в бланке ответов запишите произведение всех его корней.) . (Если уравнение имеет более
одного корня, то в бланке ответов запишите произведение всех его корней.)
Решение. Упростим левую часть уравнения:
![\log _7 (3x + 5) + \sqrt[4]{{\log _7^4 (2x + 5)}} = 0 \Leftrightarrow \log _7 (3x + 5) + |\log _7 (2x + 5)| = 0 \log _7 (3x + 5) + \sqrt[4]{{\log _7^4 (2x + 5)}} = 0 \Leftrightarrow \log _7 (3x + 5) + |\log _7 (2x + 5)| = 0](/inc/pictures/4b17f76c97e09edc2bff68fb889c028a.png) . .
Последнее уравнение равносильно совокупности двух систем:
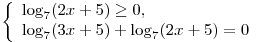 и и 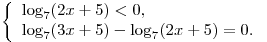
Решим первую систему:
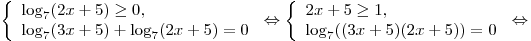
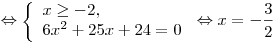 . .
Решим вторую систему:
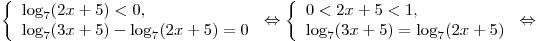
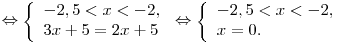
Последняя система не имеет решений.
Ответ: –1,5.
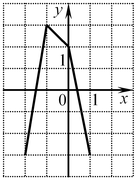 B8. Функция
B8. Функция  определена на всей
числовой прямой и является периодической с периодом 3. На рисунке
изображен график этой функции при определена на всей
числовой прямой и является периодической с периодом 3. На рисунке
изображен график этой функции при  . Найдите
значение выражения . Найдите
значение выражения 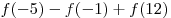 . .
Решение. Обозначим период данной функции через 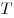 . Согласно условию . Согласно условию 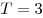 , откуда , откуда
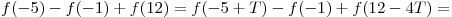
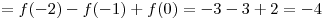 . .
Ответ: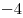 . .
B9. Две бригады работая вместе, ремонтировали дорогу в течение 6 дней, а затем одна вторая бригада закончила ремонт еще за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая
бригада, если она может выполнить эту работу на 6 дней быстрее, чем
одна вторая бригада?
Решение. Пусть  — количество дней, необходимое первой бригаде для ремонта дороги, тогда, согласно условию, второй бригаде требуется на ремонт — количество дней, необходимое первой бригаде для ремонта дороги, тогда, согласно условию, второй бригаде требуется на ремонт 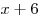 дней. Примем за 1 объем всей работы по ремонту дороги. Тогда первая бригада выполняет за день дней. Примем за 1 объем всей работы по ремонту дороги. Тогда первая бригада выполняет за день 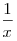 часть всей работы, а вторая — часть всей работы, а вторая — 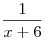 часть всей работы. Поскольку
первая бригада работала 6 дней, а вторая — 16 дней и за это время
они выполнили всю работу, получаем уравнение часть всей работы. Поскольку
первая бригада работала 6 дней, а вторая — 16 дней и за это время
они выполнили всю работу, получаем уравнение 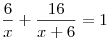 , где по смыслу задачи , где по смыслу задачи 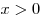 . Далее имеем: . Далее имеем:
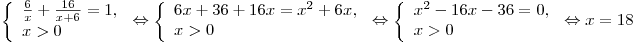 . .
Ответ: 18.
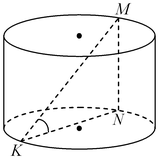 B10. Точки
B10. Точки 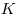 и и  лежат на окружностях двух оснований цилиндра. Синус угла наклона прямой лежат на окружностях двух оснований цилиндра. Синус угла наклона прямой 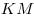 к плоскости основания цилиндра равен к плоскости основания цилиндра равен 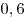 , , 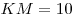 , объем цилиндра равен , объем цилиндра равен 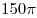 . Найдите площадь осевого сечения цилиндра. . Найдите площадь осевого сечения цилиндра.
Решение. Проведем в данном цилиндре образующую 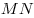 (см. рис.). Так как образующая цилиндра перпендикулярна плоскости основания, прямая (см. рис.). Так как образующая цилиндра перпендикулярна плоскости основания, прямая 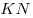 является проекцией прямой является проекцией прямой 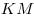 на плоскость основания цилиндра. Следовательно, угол на плоскость основания цилиндра. Следовательно, угол 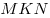 является углом наклона прямой является углом наклона прямой 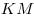 к плоскости основания цилиндра и его синус равен к плоскости основания цилиндра и его синус равен 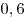 . Обозначим через . Обозначим через 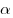 величину угла величину угла 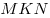 , через , через 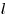 длину образующей цилиндра, через длину образующей цилиндра, через 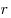 радиус его основания, через радиус его основания, через 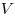 объем и через объем и через  площадь осевого сечении. Тогда имеем: площадь осевого сечении. Тогда имеем:
1. 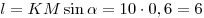 . .
2. 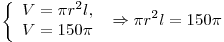 , откуда, учитывая , откуда, учитывая 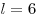 , получаем , получаем 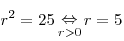 . .
3. 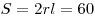 . .
Ответ: 60.
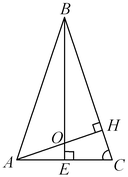 B11. Боковая сторона равнобедренного треугольника
B11. Боковая сторона равнобедренного треугольника
 равна равна 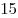 , а его площадь равна , а его площадь равна 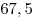 . К основанию . К основанию 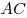 и стороне и стороне  проведены высоты проведены высоты 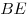 и и 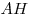 , пересекающиеся в точке , пересекающиеся в точке 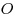 . Найдите площадь треугольника . Найдите площадь треугольника 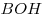 . .
Решение. Пусть  — площадь треугольника — площадь треугольника  . Тогда имеем: . Тогда имеем:
1. 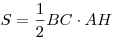 , откуда , откуда 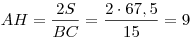 . .
2. 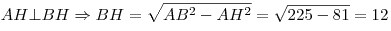 .
3. .
3. 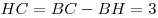 . .
4. 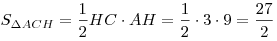 . .
5. 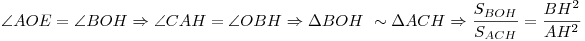 , откуда , откуда 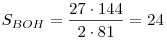 . .
Ответ: 24.
Часть C
C1. Найдите точки минимума функции 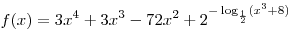 . .
Решение. Область определения данной функции совпадает с множеством решений неравенства 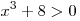 . Поскольку . Поскольку 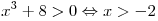 , получаем , получаем 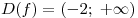 . .
На множестве 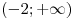 имеем: имеем:
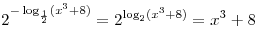 . .
Таким образом, требуется найти точки минимума функции 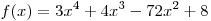 на множестве на множестве 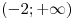 . .
Найдем производную: 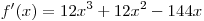 . .
Решим уравнение 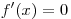 на луче на луче 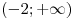 : :

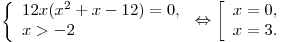
Таким образом, 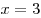 — единственная точка минимума данной функции. — единственная точка минимума данной функции.
Ответ: 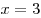 . .
| Баллы |
Критерии оценки выполнения задания С1 |
| 2 |
Приведена верная последовательность всех шагов решения:
1) нахождение области определения данной функции;
2) преобразование формулы, задающей функцию;
3) нахождение производной функции;
4) исследование функции с помощью производной.
Все тождественные преобразования и вычисления выполнены верно.
Получен верный ответ.
|
| 1 |
Приведена верная последовательность всех шагов решения.
Допущена одна описка или вычислительная ошибка, не повлиявшие на ход
решения. В результате этой описки (ошибки) может быть получен неверный
ответ.
|
| 0 |
Все случаи решения, не соответствующие критериям выставления оценок в
1 и 2 балла.
|
C2. Решите уравнение 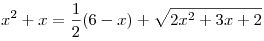 . .
Решение. Умножим обе части уравнения на 2 и перегруппируем
слагаемые:
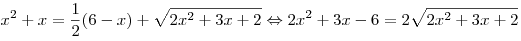 . .
Пусть 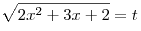 , где , где 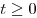 . Тогда . Тогда 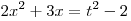 и данное уравнение принимает вид и данное уравнение принимает вид 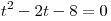 , откуда, учитывая условие , откуда, учитывая условие 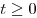 , получаем , получаем 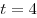 . .
Возвращаясь к переменной  , находим , находим
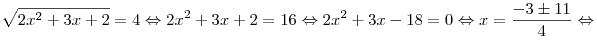
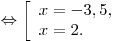
Ответ: 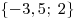 . .
| Баллы |
Критерии оценки выполнения задания С2 |
| 2 |
Приведена верная последовательность всех шагов решения:
1) замена переменной, решение полученного в результате замены
уравнения;
2) решение уравнения относительно исходной переменной, отбор корней.
Все преобразования и вычисления выполнены верно.
Получен верный ответ.
|
| 1 |
Приведена верная последовательность всех шагов решения.
Допущена одна описка или вычислительная ошибка, не повлиявшие на ход
решения. В результате этой описки (ошибки) может быть получен неверный
ответ.
|
| 0 |
Все случаи решения, не соответствующие критериям выставления оценок в
1 и 2 балла.
|
C3. Найдите все значения  , для которых при каждом , для которых при каждом  из промежутка из промежутка ![( - 3;\, - 1] ( - 3;\, - 1]](/inc/pictures/2e3068dd998f0cd9cd7bf4ba4180f225.png) значение выражения значение выражения 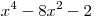 не равно значению не равно значению 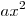 . .
Решение. Требуется найти все значения  , для которых
уравнение , для которых
уравнение 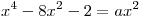 или равносильное ему
уравнение или равносильное ему
уравнение 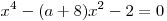 не имеет решений на
промежутке не имеет решений на
промежутке ![( - 3;\, - 1] ( - 3;\, - 1]](/inc/pictures/2e3068dd998f0cd9cd7bf4ba4180f225.png) . .
 Функция
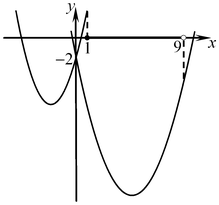
Функция 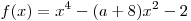 является четной, так как является четной, так как 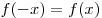 для любого для любого 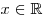 . Следовательно, эта функция не имеет корней на промежутке . Следовательно, эта функция не имеет корней на промежутке ![( -3;\, - 1] ( -3;\, - 1]](/inc/pictures/1cda91fe687527d8ddd6f20ad6bcc6d7.png) тогда и только тогда, когда она не имеет корней на промежутке тогда и только тогда, когда она не имеет корней на промежутке 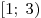 . С другой стороны, функция . С другой стороны, функция 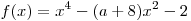 не имеет корней на множестве не имеет корней на множестве ![( - 3;\; - 1] \cup [1;\;3) ( - 3;\; - 1] \cup [1;\;3)](/inc/pictures/354f6da80f6565ac8c812642145d675a.png) тогда и только тогда, когда функция тогда и только тогда, когда функция 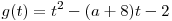 не имеет корней на промежутке не имеет корней на промежутке 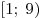 . Поскольку . Поскольку 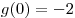 при любом значении параметра при любом значении параметра  , это условие выполняется в одном из двух случаев: либо , это условие выполняется в одном из двух случаев: либо 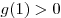 , либо , либо 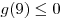 (см. рис.). (см. рис.).
Учитывая, что 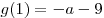 , , 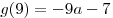 , получаем: , получаем:
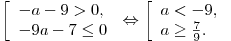
Ответ: 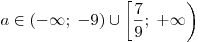 . .
| Баллы |
Критерии оценки выполнения задания С3 |
| 4 |
Приведена верная последовательность всех шагов решения:
1) получена формула, задающая функцию 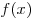 , которая не
должна иметь корней на промежутке , которая не
должна иметь корней на промежутке 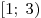 ; ;
2) обоснована четность составленной функции;
3) составлена вспомогательная функция 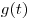 ; ;
4) установлен промежуток, на котором функция 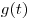 не должна
иметь корней; не должна
иметь корней;
5) найдены значения  , при которых функция , при которых функция 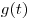 не
имеет корней на промежутке не
имеет корней на промежутке 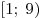 . .
Все преобразования и вычисления выполнены верно.
Получен верный ответ.
|
| 3 |
Приведена верная последовательность всех шагов решения.
Отсутствует или не обоснован шаг 2) или не обоснован шаг 4).
Допущена одна описка или вычислительная ошибка, не повлиявшие на ход
решения. В результате этой описки (ошибки) может быть получен неверный
ответ.
|
| 2 |
Верно выполнены шаги 1), 3), 4); отсутствует шаг 2); отсутствует
обоснование шага 4); шаг 5) либо не доведен до конца, либо выполнен
неверно.
Допустима описка или вычислительная ошибка.
В результате может быть получен неверный ответ.
|
| 1 |
Верно выполнены шаги 1) и 3), а остальные – либо отсутствуют,
либо выполнены неверно.
|
| 0 |
Все случаи решения, которые не соответствуют указанным выше критериям
выставления оценок в 1 – 4 балла.
|
C4. В прямоугольном параллелепипеде 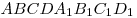 с боковыми ребрами с боковыми ребрами 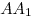 , , 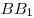 , ,
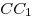 , , 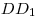 на сторонах на сторонах 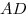 , , 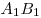 , , 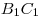 его оснований лежат соответственно
точки его оснований лежат соответственно
точки 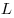 , , 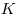 , ,  так, что так, что 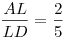 , , 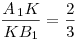 , , 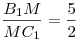 . Во сколько раз объем параллелепипеда больше объема пирамиды с вершиной . Во сколько раз объем параллелепипеда больше объема пирамиды с вершиной 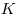 и основанием и основанием 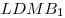 ? ?
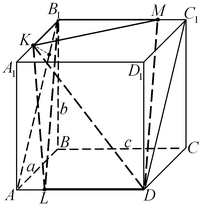 Решение. Обозначим через
Решение. Обозначим через  , ,  и и 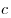 длины ребер длины ребер 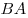 , , 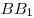 и и  параллелепипеда параллелепипеда 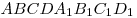 соответственно (см. рис.). Тогда объем параллелепипеда соответственно (см. рис.). Тогда объем параллелепипеда 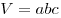 . Стороны . Стороны 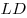 и и 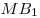 основания основания 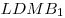 пирамиды пирамиды 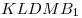 лежат на параллельных прямых лежат на параллельных прямых 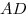 и и 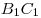 . Кроме того, по условию, . Кроме того, по условию, 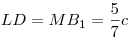 . Следовательно, . Следовательно, 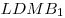 – параллелограмм. Так как – параллелограмм. Так как 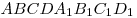 – прямоугольный параллелепипед, прямая – прямоугольный параллелепипед, прямая 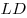 перпендикулярна плоскости, в которой лежит прямая перпендикулярна плоскости, в которой лежит прямая 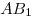 , откуда, согласно определению перпендикулярности прямой и плоскости, , откуда, согласно определению перпендикулярности прямой и плоскости, 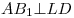 . .
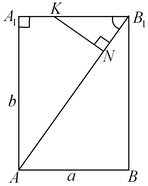 Тогда площадь основания пирамиды
Тогда площадь основания пирамиды 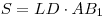 . Отрезок . Отрезок 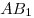 — диагональ прямоугольника — диагональ прямоугольника 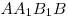 со сторонами со сторонами  и и  (см. рис.), следовательно, (см. рис.), следовательно, 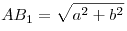 и и 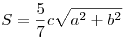 . .
Опустим перпендикуляр 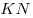 из точки из точки 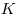 на прямую на прямую 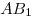 (см. рис.). Прямая (см. рис.). Прямая 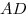 перпендикулярна плоскости перпендикулярна плоскости 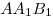 , в которой лежит прямая , в которой лежит прямая 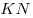 , следовательно, , следовательно, 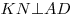 . Таким образом, прямая . Таким образом, прямая 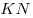 перпендикулярна двум пересекающимся прямым перпендикулярна двум пересекающимся прямым 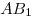 и и 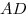 плоскости плоскости 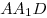 , следовательно, согласно признаку перпендикулярности прямой и плоскости, она перпендикулярна самой этой плоскости. Значит отрезок , следовательно, согласно признаку перпендикулярности прямой и плоскости, она перпендикулярна самой этой плоскости. Значит отрезок 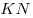 — высота пирамиды — высота пирамиды 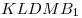 . Прямоугольные треугольники . Прямоугольные треугольники 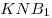 и и 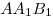 подобны, так как имеют общий острый угол подобны, так как имеют общий острый угол 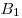 , следовательно, , следовательно, 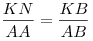 , откуда , откуда
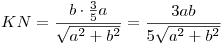 . .
Находим объем 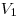 пирамиды пирамиды  : :
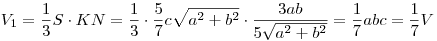 . .
Ответ: в семь раз.
| Баллы |
Критерии оценки выполнения задания С4 |
| 4 |
Приведена верная последовательность всех шагов решения:
1) обоснован тот факт, что основание пирамиды  – параллелограмм;
– параллелограмм;
2) обоснован тот факт, что отрезок 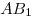 – высота
параллелограмма – высота
параллелограмма 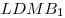 ; ;
3) обоснован тот факт, что отрезок 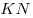 – высота пирамиды – высота пирамиды
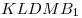 ; ;
4) доказано подобие треугольников 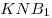 и и 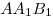 ; ;
5) вычислена площадь параллелограмма 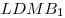 ; ;
6) вычислен объем пирамиды 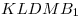 . .
Верно приведены ссылки на используемые при доказательстве положения
теории: а) определение прямой, перпендикулярной плоскости; б) признак
перпендикулярности прямой и плоскости; в) признак подобия прямоугольных
треугольников.
Все преобразования и вычисления выполнены верно. Получен верный ответ.
|
| 3 |
Приведены все шаги решения 1) – 6).
Приведены ссылки на используемые при доказательстве положения теории
а) – в). Допустимы отсутствие обоснований некоторых ключевых
моментов или неточности в обоснованиях.
Допустимы одна описка и/или вычислительная ошибка, не влияющие на
правильность дальнейшего хода решения. В результате этой ошибки или
описки может быть получен неверный ответ.
|
| 2 |
Приведены все шаги решения 1) – 6).
Ссылки на используемые при доказательстве положения теории а) –
в) либо отсутствуют, либо приведены с ошибками, но сами эти положения
теории использованы при решении.
Допустимы описки и/или вычислительные ошибки, не влияющие на
правильность дальнейшего хода решения. В результате этих ошибок или
описок может быть получен неверный ответ.
|
| 1 |
Ход решения правильный, но решение не завершено: частично приведены
шаги решения. Найдены некоторые числовые характеристики пирамиды
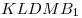 . .
Приведенные в решении обоснования и вычисления не содержат грубых
ошибок, влияющих на правильность хода решения.
|
| 0 |
Все случаи решения, которые не соответствуют указанным выше критериям
выставления оценок в 1 – 4 балла.
|
C5. Докажите, что система уравнений:
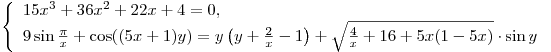
не имеет решений.
Решение. Область допустимых значений переменной  совпадает с множеством решений неравенства
совпадает с множеством решений неравенства 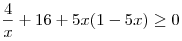 . Решим это неравенство методом интервалов: . Решим это неравенство методом интервалов:
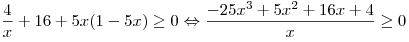 . .
Подбором находим один из корней числителя  и делим многочлен и делим многочлен 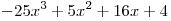 на двучлен на двучлен  с помощью схемы Горнера (можно выполнить деление, пользуясь алгоритмом деления «уголком»): с помощью схемы Горнера (можно выполнить деление, пользуясь алгоритмом деления «уголком»):
Решая получившееся квадратное уравнение, находим:
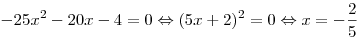 . .
Далее имеем (см. рис.):
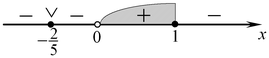
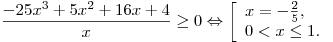
Ясно, что первое уравнение системы не имеет положительных корней, так как 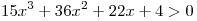 при при 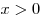 . Значит, ни одно из чисел промежутка . Значит, ни одно из чисел промежутка ![(0;\;1] (0;\;1]](/inc/pictures/9699b4065adb3a7b642055af03137f42.png) не удовлетворяет первому уравнению. Подставляя в него не удовлетворяет первому уравнению. Подставляя в него 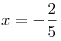 , получаем верное равенство , получаем верное равенство 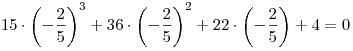 . Таким образом, . Таким образом, 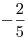 — единственное значение переменной — единственное значение переменной  , удовлетворяющее первому уравнению системы. , удовлетворяющее первому уравнению системы.
Подставив теперь 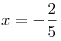 во второе уравнение системы, получаем: во второе уравнение системы, получаем:
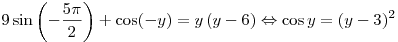 .(*) .(*)
Если 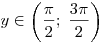 , то уравнение (*) не имеет решений, так как на
этом промежутке , то уравнение (*) не имеет решений, так как на
этом промежутке 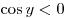 , а , а 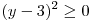 . .
Функция 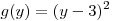 убывает на промежутке убывает на промежутке ![(-\infty ;\;3] (-\infty ;\;3]](/inc/pictures/33a8897daba91742b3768a77162e6f36.png) и возрастает на промежутке и возрастает на промежутке 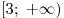 . Следовательно, если . Следовательно, если 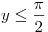 , то , то 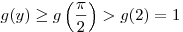 , а если , а если 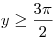 , то , то 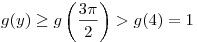 . Таким образом, . Таким образом, 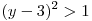 на множестве на множестве ![\left( - \infty ;\;\frac{\pi}{2} \right] \cup
\left [\frac{3\pi}{2};\; + \infty \right) \left( - \infty ;\;\frac{\pi}{2} \right] \cup
\left [\frac{3\pi}{2};\; + \infty \right)](/inc/pictures/ace018754eaebdd2f76b00e28a4995c8.png) . Так как . Так как 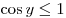 при любом значении при любом значении 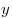 , то на множестве , то на множестве ![\left( - \infty ;\;\frac{\pi}{2} \right] \cup \left [\frac{3\pi}{2};\; + \infty \right) \left( - \infty ;\;\frac{\pi}{2} \right] \cup \left [\frac{3\pi}{2};\; + \infty \right)](/inc/pictures/985d90bf4b9fcda74af65eb764f86b39.png) уравнение (*) также не имеет решений. уравнение (*) также не имеет решений.
Итак, данная система уравнений не имеет решений, что и требовалось
доказать.
| Баллы |
Критерии оценки выполнения задания С5 |
| 4 |
Приведена верная последовательность всех шагов решения:
1) найдена область допустимых значений (ОДЗ) переменной  ; ;
2) доказано, что только число 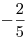 из
ОДЗ удовлетворяет первому уравнению системы; из
ОДЗ удовлетворяет первому уравнению системы;
3) доказано, что при 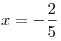 второе уравнение системы не имеет решений; второе уравнение системы не имеет решений;
Обоснованы все ключевые моменты решения:
а) отсутствие решений первого уравнения на множестве ![(0;\;1] (0;\;1]](/inc/pictures/9699b4065adb3a7b642055af03137f42.png) ; ;
б) отсутствие решений второго уравнения на множестве 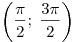 ; ;
в) отсутствие решений второго уравнения на множестве ![\left (- \infty
;\;\frac{\pi}{2} \right] \cup \left[ \frac{3\pi}{2};\; + \infty \right) \left (- \infty
;\;\frac{\pi}{2} \right] \cup \left[ \frac{3\pi}{2};\; + \infty \right)](/inc/pictures/09e5ae475b534c4f5da757a024ec13fe.png) . .
Все преобразования и вычисления выполнены верно. Сделан правильный
вывод.
|
| 3 |
Приведена верная последовательность всех шагов решения. Обоснованы все
ключевые моменты решения.
Допущена одна описка или вычислительная ошибка, не повлиявшие на ход
решения.
|
| 2 |
Верно выполнены шаги 1) и 2), а шаг 3) выполнен неверно, в том числе
– неверно обоснован.
Допустимы 1 – 2 вычислительные ошибки.
|
| 1 |
Верно выполнен шаг 1) решения, шаг 2) выполнен частично, а остальные
шаги либо отсутствуют, либо выполнены неверно.
|
| 0 |
Все случаи решения, которые не соответствуют указанным выше критериям
выставления оценок в 1 – 4 балла.
|
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

