Гущин Д. Д., Санкт-Петербург

ПРОСТРАНСТВО КАК МАТЕМАТИЧЕСКИОЕ ПОНЯТИЕ

Рассказывать школьникам о пространстве не как философской категории, а как о математическом понятии очень непросто. Об этом почти нет популярной литературы, а имеющиеся учебники адресованы студентам математических факультетов университетов. Я предлагаю свой рассказ о том, что такое пространство в математике.

Наверное, нужно начать с того, что пространство — очень объемное понятие, которому в разных контекстах придаются самые различные смыслы: вспомним хотя бы космическое, воздушное, межклеточное или информационное пространство. Конечно, разумно было бы начать с определения, однако пространство, как и любое другое основное понятие, является неопределяемым (аналогично число, множество, функция в алгебре, точка, прямая, плоскость в геометрии). Неопределяемые понятия мы можем только описывать, разъясняя, что имеется в виду, заменяя определяемое слово синонимами, обращаясь к интуиции и жизненному опыту.

Итак, под пространством понимают множество некоторых объектов, правила работы с ними и набор аксиом, которым эти правила должны подчиняться. Иными словами, это множество со введенной на нем структурой. По-разному определяя множество и структуру, мы получаем разные пространства. Из изучаемых школьном курсе можно отметить Евклидово пространство (одномерное, двумерное и трехмерное), линейное или векторное пространство и вероятностное пространство. Их элементами являются соответственно точки, векторы и элементарные события. Упоминается также четырехмерное пространство-время — пространство Минковского. (Заметим, что пространство Минковского не является четырехмерным Евклидовым пространством, поскольку имеет три пространственные и одну временную, но не пространственную, координату).

Одной из важнейших характеристик пространства является его размерность. С точки зрения аналитической геометрии, размерность фигуры равна числу координат, нужных для определения положения лежащей на этой фигуре точки; например, положение точки на кривой определяется одной координатой, на поверхности — двумя координатами, в трёхмерном пространстве — тремя координатами. (Необходимо отметить, что с середины 19 века геометрия стала изучать многомерные пространства, а в 20 веке — и пространства дробных размерностей).

Примером одномерного пространства является числовая прямая, положение каждой точки на ней можно характеризовать единственным числом. На прямой могут располагаться точки и отрезки (интервалы, полуинтервалы), они имеют одну пространственную характеристику — протяженность или длину. Примером двумерного пространства является плоскость, точки плоскости задаются двумя координатами. Плоские объекты характеризуются не только длиной, но и шириной. Примером трехмерного пространства является окружающий нас мир (Это утверждение верно до некоторых пределов. С точки зрения общей теории относительности, наш мир — искривляемое массивными телами четырехмерное пространство-время). Наряду с длиной и шириной появляется третье измерение, называемое высотой. Положение точек в трехмерном пространстве задается тремя пространственными координатами, в прямоугольной системе координат называемыми абсциссой, ординатой и аппликатой.

В рамках базовой школьной программы изучается только прямоугольная система координат. Однако необходимо отметить, что существуют и непрямоугольные системы координат, например, полярная и сферическая. В полярной системе координат на плоскости положение точки характеризуется двумя числами: расстоянием от точки до полюса и углом между полярной осью и отрезком, соединяющим точку с полюсом. Эта система координат удобна тем, что в ней уравнения некоторых линий принимают более простой вид, чем в прямоугольной системе координат. Аналогично, для задания положения точки на поверхности Земного шара понятия широты и долготы более удобны, чем какие-либо другие координаты. В сферической системе координат положение точки задают расстоянием от нее до начала координат, зенитным и азимутальным углами.

В физике используется «фазовая плоскость» — координатная плоскость, в которой по осям координат откладываются какие- либо две переменные (фазовые координаты), однозначно определяющие состояние системы. Каждому возможному состоянию системы соответствует точка фазового пространства. Изменение состояния системы отображается на фазовой плоскости движением этой точки. Фазовая плоскость является частным случаем фазового пространства, которое может иметь большую размерность. Состояние сколь угодно сложной системы представляется в фазовом пространстве одной единственной точкой, а эволюция этой системы — перемещением этой точки.

Конечно, наибольший интерес вызывает обсуждение многомерных гипертел. Приведем схему, позволяющую представить эволюцию геометрических объектов от точки до четырехмерного гиперкуба. Пусть у нас есть точка, которую мы сдвигаем вдоль прямой на некоторое расстояние. Если мы представим, что при движении точка оставляет след, то в результате сдвига мы получим отрезок. Будем теперь смещать отрезок в перпендикулярном ему направлении на расстояние, равное его длине. Результат построения — квадрат. Смещая теперь квадрат в перпендикулярном его плоскости направлению на расстояние, равное длине его стороны, получим куб. Рассуждая аналогично, мы можем вообразить четырехмерный гиперкуб. Он будет результатом смещения нашего трехмерного куба в направлении ему перпендикулярном на расстояние, равное длине любого из его ребер (см. рис. 1).

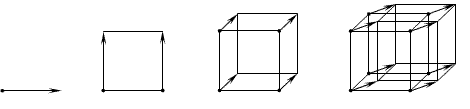
Больше того, наш алгоритм позволяет заметить геометрические характеристики гиперкуба! Проследим поэтапно: начальное и конечное положение движущейся точки обусловили наличие двух вершин отрезка. В свою очередь, четыре вершины квадрата образовались из двух вершин исходного и еще двух — смещенного отрезка. Число вершин куба представляет собой сумму числа вершин исходного и смещенного квадратов, поэтому их восемь, а число вершин гиперкуба будет равно шестнадцати — это вершины исходного и смещенного кубов. (Заметим, что число вершин 2, 4, 8, 16… является геометрической прогрессией.)

Продолжим наши наблюдения за объектом, который мы не в силах представить, но можем охарактеризовать. Единственная «сторона» отрезка — результат движения точки. Четыре стороны квадрата складываются из начального и конечного отрезков и еще двух отрезков, соединяющих исходные, и полученные смещением вершины этого отрезка. Поэтому же число ребер куба равно 12 (это по 4 стороны исходного и смещенного квадратов и еще 4 ребра, соединяющие соответствующие вершины исходного и смещенного). Аналогично число ребер гиперкуба — 32 (это по 12 ребер исходного и смещенного кубов и еще 8 ребер, образованных при движении 8 вершин исходного куба).

Далее, у нашего трехмерного куба 6 плоских граней — это исходный и смещенный квадраты, а также квадраты, полученные движением 4 сторон исходного квадрата. Аналогично число плоских граней гиперкуба — 24: по 6 граней у исходный и смещенного кубов, и еще 12, полученных движением 12 ребер исходного куба. Помимо 24 плоских граней, гиперкуб будет иметь еще 8 кубических граней: действительно, отрезок ограничен 2 точками, квадрат — 4 сторонами, куб — 6 гранями, гиперкуб — 8 кубами и т. д.; числа 2, 4, 6, 8… образуют арифметическую прогрессию. (Продолжая, мы можем рассматривать пятимерный гиперкуб. Он имеет 32 вершины, 80 ребер, 80 квадратных, 40 кубических и 10 гиперкубических граней. И так далее.)

При всей схожести построения объектов, пространства, в которых они существуют совсем разные.

Рассмотрим мир жителей прямой. Вне прямой для них ничего не существует, просто ничего нет, даже пустоты. Внутри этого мира органами зрения можно видеть лишь точки. Это сами точки, или перпендикулярные проекции отрезков (представьте, что мы смотрим на иголку со стороны острия). Движение возможно только между двумя объектами на прямой, так как обойти точки, не сходя с этой нее, невозможно (см. рис. 2).

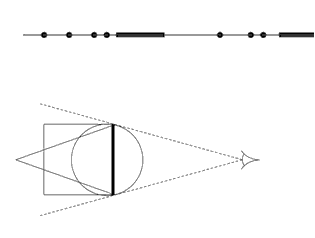
Двумерный мир представляет собой плоскость. Обитатели этого мира — точки, отрезки, плоские фигуры. Глядя друг на друга, они могут видеть лишь отрезки, которыми являются проекции плоских фигур на прямую (см. рис. 3).

Трехмерный мир окружает нас. Мы привыкли к нему, объекты, окружающие нас трехмерны, хоть в каждый момент времени мы видим только их плоские проекции — как на фотографии. Если бы мы были четырехмерными, в трехмерном мире перед нами открылись самые фантастические возможности.

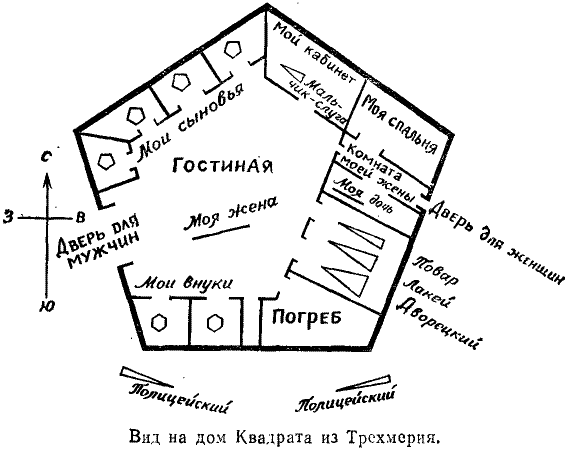
Например, рассматривая плоский мир рисунка (см. [3], стр. 101), мы видим внутренность всех комнат, равно как и их обитателей и всего дома (см. рис. 4). Аналогично мы увидели бы улицы, горы и пещеры, извилистые лабиринты и спрятанные тайники, небеса и подземелья — все открывается взгляду и видно насквозь. Один из героев книги — Сфера — является перед жителем плоского мира Флатландии и пытается доказать ему существование неизвестного тому третьего измерения. Для убедительности со словами «… легкая боль, которую вы, быть может, ощутите, не идет ни в какое сравнение с выгодой, извлекаемой из этого прикосновения вашим умом», трехмерная Сфера даже касается желудка двумерного квадрата» [3, стр. 98].

Итак, из следующего измерения мы получаем возможность видеть насквозь все, происходящее в пространстве меньшей размерности, возможность беспрепятственно перемещать предметы сквозь границы, видоизменяться в пространствах меньшей размерности, появляясь в них тем или иным своим многомерным сечением, исчезать в одной точке и появляться в другой точке беспричинно и непредсказуемо для обитателей меньших размерностей. В этом, несмотря на всю непохожесть, наши пространства имеют много общего.

Сила и красота математики, ее абстрактность и универсальность состоят как раз в том, что она находит универсальные единые методы описания пространств, что используемый язык позволяет строить плодотворные модели и аналогии для самых непохожих на первый взгляд объектов.

Литература:

[1] Смирнова И. М., Смирнов В. А. Геометрия 10-11 . — М., «Просвещение», 2001.

[2] http://ru.wikipedia.org/wiki/Тессеракт

[3] Эбботт Э. Э. Флатландия, Бюргей Д. Сферландия. — М., «Мир», 1976.

Наверх