|
Единый государственный экзамен по математике, 2001 год
Часть A
A1. Найдите значение выражения 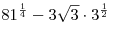 . .
Решение. Используя свойства степени получаем:
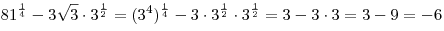 . .
Правильный ответ: 1.
A2. Упростите выражение ![\frac{{\sqrt[3]{{a^2 }} - 16}}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} \frac{{\sqrt[3]{{a^2 }} - 16}}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a}](/inc/pictures/dfd77716f3a2b297063d2c2146a70ece.png) . .
Решение. Используя свойства арифметического корня последовательно получаем:
![\frac{{\sqrt[3]{{a^2 }} - 16}}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} = \frac{{(\sqrt[3]{a})^2 - 4^2 }}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} = \frac{{(\sqrt[3]{a} - 4)(\sqrt[3]{a} + 4)}}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} = \frac{{\sqrt[3]{{a^2 }} - 16}}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} = \frac{{(\sqrt[3]{a})^2 - 4^2 }}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} = \frac{{(\sqrt[3]{a} - 4)(\sqrt[3]{a} + 4)}}{{\sqrt[3]{a} - 4}} - \sqrt[3]{a} =](/inc/pictures/d582404dbae0546d96093aa281fa6fb4.png)
![= \sqrt[3]{a} + 4 - \sqrt[3]{a} = 4 = \sqrt[3]{a} + 4 - \sqrt[3]{a} = 4](/inc/pictures/24eddb5272f5940d3cf9049a7f49f4f3.png) . .
Правильный ответ: 2.
A3. Упростите выражение 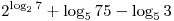 . .
Решение. Используя основное логарифмическое тождество и формулу преобразования разности логарифмов в логарифм частного, получаем:
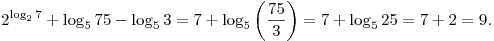
Правильный ответ: 1.
A4. Решите неравенство 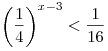 . .
Решение. Перейдем к одному основанию и воспользуемся убыванием показательной функции с основанием меньшим единицы:
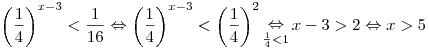 . .
Правильный ответ: 3.
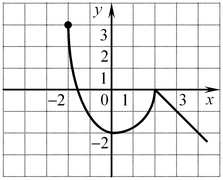
A5. Укажите промежуток возрастания функции  , заданной графиком. , заданной графиком.
Решение. Функция убывает на промежутках ![[ - 2;\,0] [ - 2;\,0]](/inc/pictures/4c85c6d1ee3084645622853c31dffdd8.png) и и 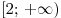 . Функция возрастает на промежутке . Функция возрастает на промежутке ![[0;\,2] [0;\,2]](/inc/pictures/fc0441ee3fa76e443cde8129362cf539.png) . .
Правильный ответ: 4.
A6. Упростите выражение 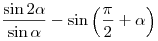 . .
Решение. Используя формулу синуса двойного аргумента и формулу приведения, получим:
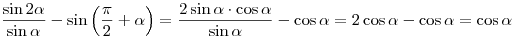 . .
Правильный ответ: 2.
A7. Найдите производную функции 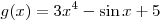 . .
Решение. Используя формулы 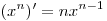 , , 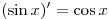 и и 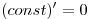 , получим: , получим:
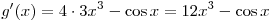 . .
Правильный ответ: 1.
A8. Укажите промежуток, которому принадлежит корень уравнения 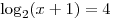 . .
Решение. Решим уравнение:
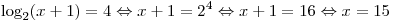 . .
Корень уравнения принадлежит промежутку 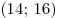 . .
Правильный ответ: 2.
A9. Найдите область определения функции 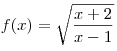 . .
Решение. Область определения функции задается неравенством 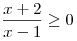 . Решим его методом интервалов. . Решим его методом интервалов.
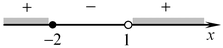
Видно, что 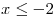 ; ; 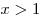 . .
Правильный ответ: 3.
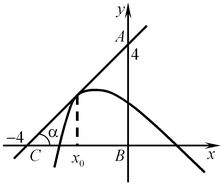
A10. Найдите значение производной функции  в точке в точке 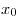 . .
Решение. Значение производной в точке касания равно тангенсу угла наклона касательной, проведенной в этой точке. Найдем 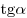 из треугольника из треугольника  (см. рис.): (см. рис.): 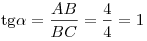 . .
Правильный ответ: 4.
A11. Найдите наименьшее значение функции 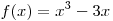 на отрезке на отрезке ![[0; \,3] [0; \,3]](/inc/pictures/aaac8747540c43816a65eb5028b5115f.png) . .
Решение. Найдем критические точки данной функции на отрезке ![[0; \,3] [0; \,3]](/inc/pictures/aaac8747540c43816a65eb5028b5115f.png) . Производная заданной функции есть . Производная заданной функции есть 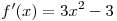 , решениями уравнения , решениями уравнения 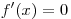 являются числа являются числа 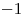 и и 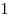 , из них отрезку , из них отрезку ![[0; \,3] [0; \,3]](/inc/pictures/aaac8747540c43816a65eb5028b5115f.png) принадлежит только число принадлежит только число 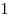 .
Вычислим значения функции в точке .
Вычислим значения функции в точке  и на концах отрезка и на концах отрезка ![[0; \,3] [0; \,3]](/inc/pictures/aaac8747540c43816a65eb5028b5115f.png) и выберем из них наименьшее: и выберем из них наименьшее: 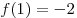 , , 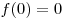 , , 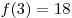 . Тогда искомое наименьшее значение есть . Тогда искомое наименьшее значение есть 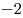 . .
Правильный ответ: 3.
A12. Найдите площадь фигуры, ограниченной линиями: 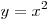 , , 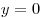 , , 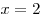 . .
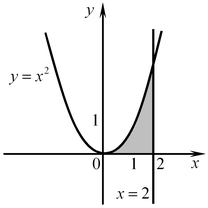
Решение. Нарисуем эскизы графиков функций 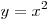 , , 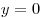 , , 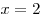 . Фигура, площадь которой требуется найти, на рисунке заштрихована. Площадь этой фигуры . Фигура, площадь которой требуется найти, на рисунке заштрихована. Площадь этой фигуры  находим по формуле находим по формуле 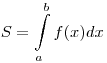 : :
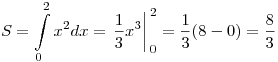 . .
Правильный ответ: 2.
A13. Решите уравнение 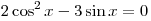 . .
Решение. Используя основное тригонометрическое тождество, приведем уравнение к квадратному относительно 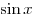 и решим его: и решим его:
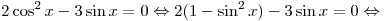
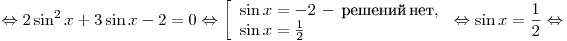
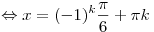 , , 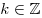 . .
Правильный ответ: 2.
Часть B
B1. Решите уравнение 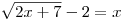 . .
Решение. Используя теорему 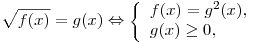 получим: получим:
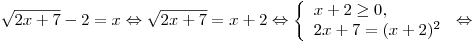
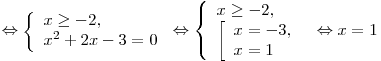 . .
Ответ: 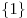 . .
B2. Найдите значение выражения 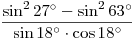 . .
Решение. (I способ). Воспользуемся формулами приведения и формулами косинуса и синуса двойного аргумента: 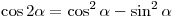 и и 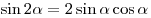 . Имеем . Имеем
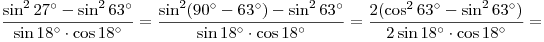
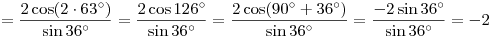 . .
Решение. (II способ). Используем формулу понижения степени 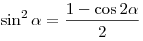 . Имеем . Имеем
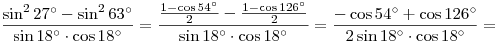
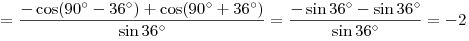 . .
Ответ: 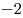 . .
B3. Найдите точку максимума функции 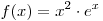 . .
Решение. Найдем производную данной функции:
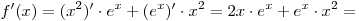
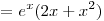 . .
Найдем нули производной:
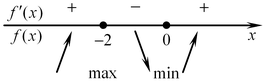
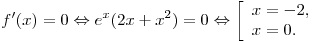
Поведение функции изображено на рисунке. Максимум функции достигается в точке 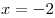 . .
Ответ: точка максимума: 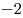 . .
B4. Найдите меньший корень уравнения 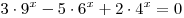 . .
Решение. Данное уравнение является однородным относительно выражений 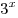 и и 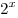 . Так как . Так как 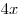 не равно нулю ни при каких значениях не равно нулю ни при каких значениях  , разделив левую и правую часть уравнения на , разделив левую и правую часть уравнения на 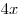 , получаем: , получаем:
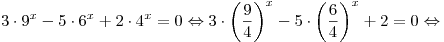
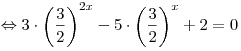 . (*) . (*)
Пусть 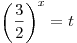 . Тогда уравнение (*) принимает вид . Тогда уравнение (*) принимает вид 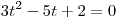 . Далее имеем: . Далее имеем:
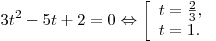
Таким образом,
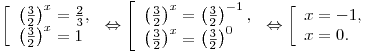
Итак, меньший корень уравнения равен 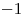 . .
Ответ: 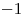 . .
B5. Катер прошел по течению реки расстояние от пункта  до пункта до пункта  за за 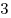 ч, а от ч, а от  до до  — за — за 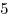 ч. За сколько часов проплывет от ч. За сколько часов проплывет от  до до  плот? плот?
Решение. Пусть  — расстояние между — расстояние между  и и  , , 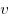 — скорость катера, — скорость катера, 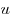 — скорость течения реки ( — скорость течения реки (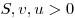 , , 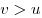 ). При движении из ). При движении из  в в  скорость катера была скорость катера была 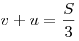 , при движении из , при движении из  в в  скорость была скорость была 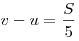 . Решим систему: . Решим систему:
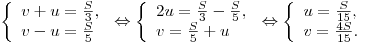
Таким образом, скорость течения реки равна 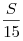 , и плот, движущийся со скоростью реки, пройдет пусть от , и плот, движущийся со скоростью реки, пройдет пусть от  до до  за за 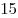 часов. часов.
Ответ: 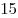 часов. часов.
B6. Найдите число целых решений неравенства 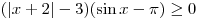 . .
Решение. Поскольку второй множитель, в силу ограничения 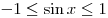 , отрицателен при всех значениях , отрицателен при всех значениях  , имеем неравенство: , имеем неравенство:
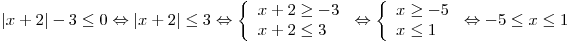 . .
Таким образом, неравенство имеет 5 отрицательных целых решений, одно положительное и решение 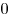 . Всего их 7. . Всего их 7.
Ответ: 7 штук.
B7. Найдите наибольшее целое значение параметра 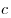 , при котором решение системы уравнений , при котором решение системы уравнений 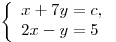 удовлетворяет неравенству удовлетворяет неравенству 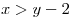 . .
Решение. Решим систему
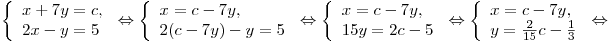
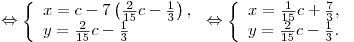
Решим неравенство 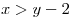 : :
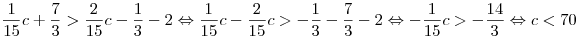 . .
Наибольшим целым значением c, удовлетворяющим неравенству 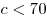 , является число 69. , является число 69.
Ответ: 69.
B8. Высота правильной треугольной пирамиды равна 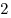 , двугранные углы при основании равны , двугранные углы при основании равны 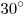 . Найдите площадь боковой поверхности пирамиды. . Найдите площадь боковой поверхности пирамиды.
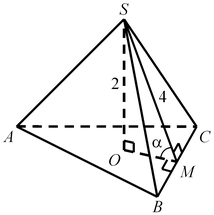 Решение. Пусть
Решение. Пусть 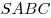 — заданная пирамида (см. рисунок), — заданная пирамида (см. рисунок), 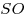 — ее высота, — ее высота, 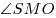 — линейный угол двугранного угла при основании. Поскольку — линейный угол двугранного угла при основании. Поскольку 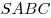 — правильная пирамида, основание — правильная пирамида, основание 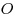 ее высоты есть центр окружности, вписанной в треугольник ее высоты есть центр окружности, вписанной в треугольник  , следовательно, , следовательно, 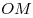 — радиус этой окружности, откуда — радиус этой окружности, откуда 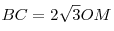 . Из прямоугольного треугольника . Из прямоугольного треугольника 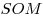 находим находим 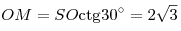 , , 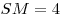 . Тогда . Тогда 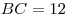 . .
Окончательно получаем
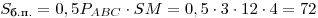 . .
Ответ: 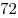 . .
B9. В конус с радиусом основания 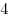 и высотой и высотой 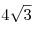 вписана треугольная призма, у которой все ребра равны. Найдите объем призмы. вписана треугольная призма, у которой все ребра равны. Найдите объем призмы.
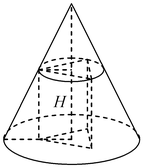 Решение. Пусть ребро призмы равно
Решение. Пусть ребро призмы равно  , пусть окружность, описанная около верхнего основания — правильного треугольника — имеет радиус , пусть окружность, описанная около верхнего основания — правильного треугольника — имеет радиус 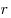 . Тогда ребро призмы есть . Тогда ребро призмы есть 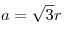 . .
Отношение площади сечения, параллельного основанию конуса, к площади основания равно отношению квадратов их расстояний до вершины конуса, откуда последовательно получаем
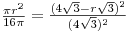 , , 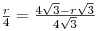 , , 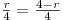 , , 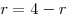 , , 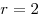 . .
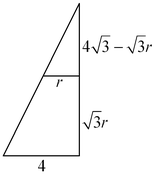
Тогда 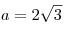 , откуда объем призмы равен: , откуда объем призмы равен:
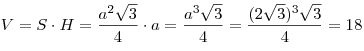 . .
Ответ: 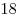 . .
Часть C
C1. Для каждого допустимого значения параметра 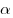 решите неравенство решите неравенство
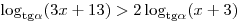 . .
Решение.
1. Если 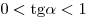 , то , то 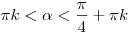 , , 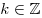 , и мы имеем: , и мы имеем:
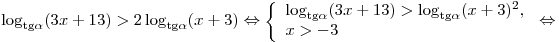
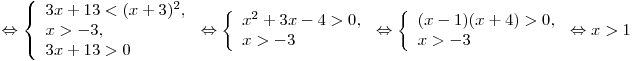 . .
2. Если 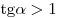 , то , то 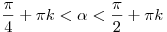 , , 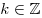 и тогда: и тогда:
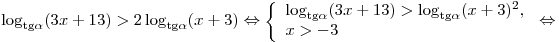
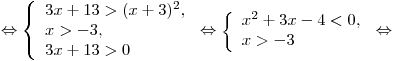
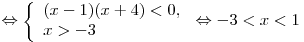 . .
Ответ: 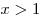 при при 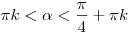 , , 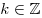 ; ; 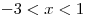 при при 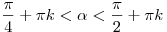 , , 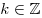 . .
C2. Решите уравнение 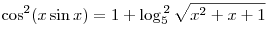 . .
Решение. Левая часть уравнения не больше, а правая — не меньше единицы, следовательно, данное уравнение равносильно системам:
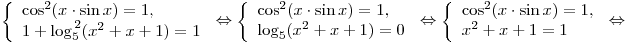
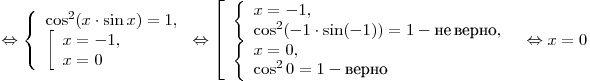 . .
Ответ: 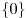 . .
C3. Найдите целые корни уравнения 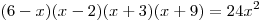 . .
Решение.
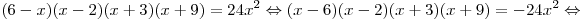
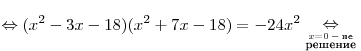
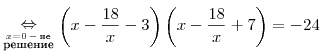 . (*) . (*)
Пусть 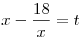 . Тогда уравнение (*) принимает вид . Тогда уравнение (*) принимает вид 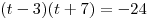 , откуда получаем , откуда получаем
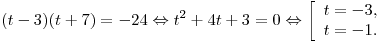
Таким образом,
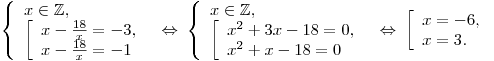
Ответ: 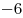 ; ; 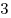 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
