Правильные многогранники
Выпуклый многогранник называется правильным, если все его грани
— равные правильные многоугольники, и в каждой его вершине
сходится одно и то же число ребер.
Все ребра правильного многогранника равны, все двугранные углы
правильного многогранника равны, все многогранные углы правильного
многогранника равны. Существует ровно пять выпуклых правильных
многогранников:
Выпуклый многогранник называется правильным, если его грани
являются правильными многоугольниками с одним и тем же числом сторон, и
в каждой вершине многогранника сходится одно и то же число ребер.
Все ребра правильного многогранника равны друг другу. Равны также все
его двугранные углы, содержащие две грани с общим ребром.
Грани правильного многогранника могут быть либо равносторонними
треугольниками, либо квадратами, либо правильными пятиугольниками.
Действительно, угол правильного  -угольника при -угольника при
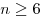 не меньше не меньше 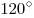 . С другой стороны, при каждой
вершине многогранника должно быть не менее трех плоских углов. Поэтому
если бы существовал правильный многогранник, у которого грани –
правильные n-угольники при . С другой стороны, при каждой
вершине многогранника должно быть не менее трех плоских углов. Поэтому
если бы существовал правильный многогранник, у которого грани –
правильные n-угольники при 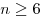 , то сумма плоских углов
при каждой вершине такого многогранника была бы не меньше чем , то сумма плоских углов
при каждой вершине такого многогранника была бы не меньше чем
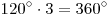 . Но это невозможно, так как
сумма всех плоских углов при каждой вершине выпуклого многогранника
меньше . Но это невозможно, так как
сумма всех плоских углов при каждой вершине выпуклого многогранника
меньше 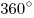 . .
По этой же причине каждая вершина правильного многогранника может быть
вершиной либо трех, четырех или пяти равносторонних треугольников, либо
трех квадратов, либо трех правильных пятиугольников. Других
возможностей нет.
Правильный тетраэдр (четырехгранник) — многогранник,
составленный из четырех правильных треугольников (рис.1а).
Правильный гексаэдр (шестигранник) или куб —
многогранник, составленный из шести правильных четырехугольников
(квадратов) (рис. 1б).
Правильный октаэдр (восьмигранник) — многогранник,
составленный из восьми правильных треугольников (рис. 1в).
Правильный додекаэдр (двенадцатигранник) — многогранник,
составленный из двенадцати правильных пятиугольников (рис. 1г).
Правильный икосаэдр (двадцатигранник) — многогранник,
составленный из двадцати правильных треугольников (рис. 1д).

 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
