Пирамида
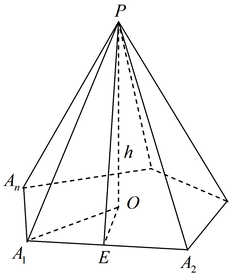
Пирамидой называется многогранник одна из граней которого
является произвольным многоугольником, а остальные грани —
треугольники, имеющие общую вершину.
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания,
называется высотой пирамиды.
Тетраэдр — это пирамида, в основании которой лежит
треугольник.
Треугольники, из которых состоит тетраэдр, называются его
гранями, их стороны — ребрами, а вершины —
вершинами тетраэдра. Два ребра тетраэдра, не имеющие общих
вершин, называются противоположными. Обычно выделяют одну из
граней тетраэдра и называют ее основанием, а остальные грани
называют боковыми гранями.
Правильным тетраэдром называют тетраэдр у которого все ребра
равны.
Правильной пирамидой называется такая пирамида, если ее основание
— правильный многоугольник, а основание высоты пирамиды совпадает
с центром этого многоугольника. Прямая, содержащая высоту
правильной пирамиды называется ее осью.
Высота боковой грани правильной пирамиды, проведенная из ее вершины,
называется апофемой.
Усеченная пирамида (см. далее) называется правильной, если она
получена сечением правильной пирамиды плоскостью, параллельной
основанию. Основания правильной усеченной пирамиды – правильные
многоугольники, а боковые грани – равнобедренные трапеции. Высоты
этих трапеций называются апофемами усеченной пирамиды.
Свойства пирамиды:
Рассмотрим следующие утверждения:
Боковые ребра пирамиды равны.
Боковые ребра пирамиды одинаково наклонены к основанию пирамиды.
Вершина пирамиды проектируется в центр окружности, описанной около
основания пирамиды.
Высоты всех боковых граней пирамиды, проведенные из вершины пирамиды,
равны, а высота пирамиды лежит внутри пирамиды.
Все двугранные углы при основании пирамиды равны.
Вершина пирамиды проектируется в центр окружности, вписанной в
основание пирамиды.
В правильной треугольной пирамиде противоположные ребра попарно
перпендикулярны.
Если боковые ребра пирамиды равны между собой, то в основании лежит
правильный многоугольник, вокруг которого можно описать окружность, а
вершина пирамиды проецируется в центр этой окружности.
Если двугранные углы при основании пирамиды равны между собой, то в
основании пирамиды лежит многоугольник, в который можно вписать
окружность, а вершина пирамиды проецируется в центр этой окружности.
Утверждения 1, 2, 3 и 4, 5, 6 равносильны.
Сечение пирамиды плоскостью, параллельной
основанию
Сечение пирамиды плоскостью, параллельной ее основанию
(перпендикулярной высоте) делит высоту и боковые ребра пирамиды на
пропорциональные отрезки.
Сечение пирамиды плоскостью, параллельной ее основанию
(перпендикулярной высоте) есть многоугольник, подобный основанию
пирамиды, причем коэффициент подобия этих многоугольников равен
отношению их расстояний от вершины пирамиды.
Площади сечений, параллельных основанию пирамиды, относятся как
квадраты их расстояний от вершины пирамиды.
Площадь поверхности и объём пирамиды
Пусть 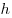 — высота пирамиды, — высота пирамиды, 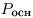 — периметр основания пирамиды,
— периметр основания пирамиды, 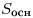 —
площадь основания пирамиды, —
площадь основания пирамиды, 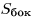 — площадь
боковой поверхности пирамиды, — площадь
боковой поверхности пирамиды, 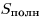 — площадь
полной поверхности пирамиды, — площадь
полной поверхности пирамиды, 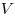 — объем пирамиды. Тогда
имеют место следующие соотношения: — объем пирамиды. Тогда
имеют место следующие соотношения:
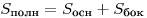
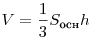
Если все двугранные углы при основании пирамиды равны 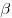 , а высоты всех боковых граней пирамиды, проведенные из вершины
пирамиды, равны , а высоты всех боковых граней пирамиды, проведенные из вершины
пирамиды, равны 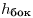 , то , то
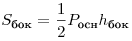
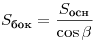
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
