|
Окружность и ее элементы
Окружность — множество всех точек плоскости, удаленных на заданное расстояние (равное радиусу) от заданной точки этой же плоскости (центра окружности).
Радиусы — отрезки, соединяющие точки окружности с центром. Все радиусы данной окружности равны.
Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр — хорда, проходящая через центр окружности. Диаметр, делящий хорду пополам, перпендикулярен этой хорде.
Центральный угол — угол, образованный двумя радиусами. Центральный угол измеряется дугой, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны являются ее хордами.
Касательная — прямая, проходящая через точку окружности, перпендикулярно ее радиусу. Касательная имеет с окружностью только одну общую точку.
Длина окружности: 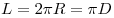 , , 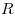 — радиус окружности, — радиус окружности, 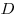 — диаметр. — диаметр.
Длина дуги окружности: 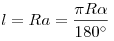 , ,  — радианная мера дуги, — радианная мера дуги, 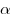 — градусная мера. — градусная мера.
Круг — часть плоскости, ограниченная окружностью.
Площадь круга: 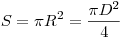 . .
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности.
Площадь сектора: 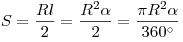 . .
Сегмент – часть круга, ограниченная хордой и дугой.
Площадь сегмента: 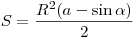 (или (или 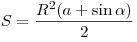 , если центр круга лежит внутри сегмента). , если центр круга лежит внутри сегмента).
Свойства вписанных углов
- Вписанный угол измеряется половиной дуги, на которую он опирается:
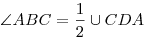 . .
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на диаметр — прямой.
- Равные дуги окружности стягиваются равными хордами.
Углы, связанные с окружностью
Теорема (угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг: 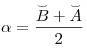 . .
Теорема (угол между секущими). Угол между двумя секущими, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг: 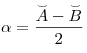 . .
Теорема (угол между касательной и хордой, проведенной через точку
касания). Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой: 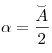 . .
Теорема (угол между касательной и секущей). Угол между касательной и секущей равен полуразности высекаемых ими дуг:
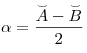 . .
Теорема (угол между касательными). Угол между двумя касательными, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг: 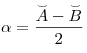 . .
Отрезки, связанные с окружностью
Теорема. Отрезки касательных к окружностям, проведенным из одной точки, равны: 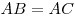 , центр окружности лежит на биссектрисе угла , центр окружности лежит на биссектрисе угла 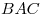 . .
Теорема. Произведение секущей на ее внешнюю часть есть для данной окружности величина постоянная и равная разности квадратов расстояния от точки пересечения секущих до центра окружности и радиуса окружности: [Unparseable or potentially dangerous latex formula. Error 3 ].
Теорема. Произведение отрезков, на которые делится хорда данной
точкой, есть для данной окружности величина постоянная: [Unparseable or potentially dangerous latex formula. Error 3 ] и равна разности квадратов радиуса окружности и расстояния от
точки  до центра окружности. до центра окружности.
Теорема. Квадрат касательной равен произведению секущей на ее внешнюю часть: [Unparseable or potentially dangerous latex formula. Error 3 ].
Теорема. Отношение хорды к синусу вписанного угла, который на нее опирается, равно двум радиусам (теорема синусов): [Unparseable or potentially dangerous latex formula. Error 3 ].
Теорема Птолемея: Во всяком четырехугольнике, вписанном в
окружность, сумма произведений длин противоположных сторон равна
произведению длин его диагоналей: 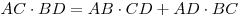 . .
Окружность, вписанная в многоугольник
Если все стороны многоугольника касаются окружности, то окружность
называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
Теоремы:
- Центром вписанной в четырехугольник окружности является точка
пересечения биссектрис (если она биссектрисы всех его углов
пересекаются в одной точке).
- В любом описанном четырехугольнике суммы противоположных сторон равны.
- Если суммы противоположных сторон выпуклого четырехугольника равны, то
в него можно вписать окружность.
- Из параллелограммов окружность можно вписать в ромб, квадрат.
- Если в трапецию вписана окружность, то сумма оснований равна сумме
боковых сторон, а средняя линия — полусумме боковых сторон:
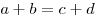 , , 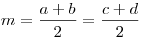 . .
Окружность, описанная около четырехугольника
Если вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.
Теоремы:
- Центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам.
- В любом четырехугольнике, вписанном в окружность, сумма противоположных углов равна
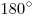 . .
- Из всех параллелограммов окружность можно описать около
прямоугольника, квадрата.
Вневписанная окружность
Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других его сторон.
Теорема. Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно полупериметру p: 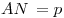 . .
Примечание: точка касания вневписанной окружности со стороной
треугольника делит его периметр пополам: 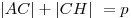 . .
Следствие: 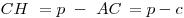 , , 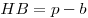 . .
Теорема. Радиус вневписанной окружности, проведенный к стороне a, вычисляется по формуле: 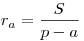 . .
Теорема. Площадь треугольника, можно вычислить по формуле: 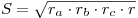 , где , где 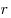 — радиус вписанной окружности; — радиус вписанной окружности; 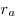 — радиус вневписанной окружности, проведенный к стороне a; — радиус вневписанной окружности, проведенный к стороне a; 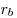 — радиус вневписанной окружности, проведенный к стороне b; — радиус вневписанной окружности, проведенный к стороне b; 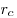 — радиус вневписанной окружности, проведенный к стороне с. — радиус вневписанной окружности, проведенный к стороне с.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
