|
Треугольники и их элементы
Треугольник — это замкнутая ломаная, состоящая из трех звеньев, и часть плоскости, ею ограниченная (рис. 1).
Обозначения:
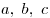 — длины сторон — длины сторон 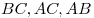 треугольника треугольника  соответственно; соответственно;
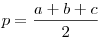 — полупериметр треугольника — полупериметр треугольника  ; ;
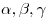 — величины углов — величины углов 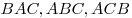 треугольника треугольника  соответственно; соответственно;
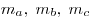 — длины медиан — длины медиан 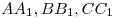 треугольника треугольника  соответственно; соответственно;
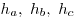 — длины высот — длины высот 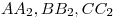 треугольника треугольника  соответственно; соответственно;
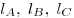 — длины биссектрис — длины биссектрис 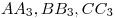 треугольника треугольника  соответственно; соответственно;
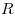 — радиус окружности, описанной около треугольника — радиус окружности, описанной около треугольника  ; ;
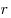 — радиус окружности, вписанной в треугольник — радиус окружности, вписанной в треугольник  ; ;
 — площадь треугольника — площадь треугольника  . .
Элементы треугольника
Сторона треугольника — отрезок, соединяющий две его вершины.
Неравенство треугольника — в любом треугольнике сумма длин двух сторон больше длины третьей стороны: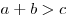 , , 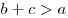 , , 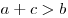 . .
Пусть 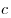 — наибольшая из трех сторон треугольника, тога если — наибольшая из трех сторон треугольника, тога если 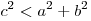 , то треугольник остроугольный; если , то треугольник остроугольный; если 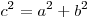 , то треугольник прямоугольный; если , то треугольник прямоугольный; если 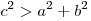 , то треугольник тупоугольный. , то треугольник тупоугольный.
Угол — часть плоскости, ограниченная двумя лучами, выходящими из вершины.
Теорема. Сумма углов треугольника равна 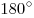 : :
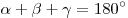 . .
Следствие: В треугольнике не может быть более одного тупого или
прямого угла.
Внешний угол — угол, смежный с каким-нибудь углом треугольника (рис. 2).
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Биссектриса угла — прямая, делящая угол на две равные части.
Биссектриса угла треугольника — наибольший отрезок биссектрисы угла, лежащий внутри треугольника.
Теорема. Если точка лежит на биссектрисе треугольника, то она
равноудалена от сторон угла.
Верно и обратное утверждение: если точка равноудалена от сторон угла, то она лежит на биссектрисе угла этого треугольника.
Биссектрисы треугольника пересекаются в одной точке, называемой инцентром, и являющейся центром вписанной в этот треугольник
окружности (рис.3). Радиус вписанной в треугольник окружности может
быть найден по формулам: 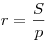 , , 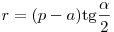 . .
Медиана — это отрезок, соединяющий какую-либо вершину треугольника с серединой противоположной стороны.
Теорема. Медианы треугольника пересекаются в одной точке,
называемой центроидом треугольника, и являющейся центром тяжести
этого треугольника.
Высота — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Высоты треугольника пересекаются в одной точке, называемой ортоцентром. Длины высот находятся по следующим формулам:
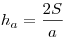 , , 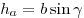 . .
Биссектриса угла треугольника лежит между медианой и высотой, проведенной из той же вершины, что и сама биссектриса (рис. 4).
Средняя линия треугольника — это отрезок, соединяющий
середины двух его сторон.
Теорема. Средняя линия треугольника, соединяющая середины двух
его сторон, параллельна третьей стороне и равна ее половине: [Unparseable or potentially dangerous latex formula. Error 3 ], 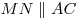 (рис. 5).
(рис. 5).
Серединный перпендикуляр к отрезку — прямая, перпендикулярная к этому отрезку и проходящая через его середину.
Теорема. Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от его концов.
Верно и обратное утверждение: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.
Все три серединных перпендикуляра пересекаются в одной точке, являющейся центром окружности, описанной вокруг треугольника (рис. 6).
Если треугольник остроугольный, центр описанной окружности лежит строго внутри треугольника. Если треугольник прямоугольный, центр описанной окружности лежит на середине гипотенузы. Если треугольник тупоугольный, центр описанной окружности лежит вне треугольника.
Радиус описанной окружности может быть найден по формулам: 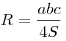 , , 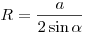 . .
Три замечательные точки треугольника: центр описанной
окружности, точка пересечения медиан и точка пересечения высот лежат на
одной прямой. Эта прямая называется прямой Эйлера.
Теорема синусов. Отношение длины стороны треугольника к синусу
противолежащего угла для данного треугольника есть величина постоянная
и равная диаметру описанной около треугольника окружности:
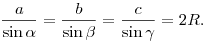
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: 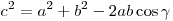 . .
Теорема тангенсов. Разность двух сторон треугольника относится
к их сумме, как тангенс полуразности противолежащих углов к тангенсу их
полусуммы: 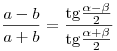 . .
Признаки подобия треугольников
Подобными называются треугольники, у которых углы равны, а сходственные стороны пропорциональны: 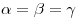 , , 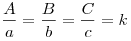 , где , где
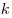 — коэффициент подобия (рис. 7). — коэффициент подобия (рис. 7).
I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.
II признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то
такие треугольники подобны.
III признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Следствие: Площади подобных треугольников относятся как квадрат
коэффициента подобия: 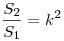 . .
Признаки равенства треугольников
Равными называют треугольники, у которых соответствующие стороны равны.
Теорема (первый признак равенства треугольников).
Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны.
Теорема (второй признак равенства треугольников).
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема (третий признак равенства треугольников).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Медиана треугольника
Медиана — отрезок, соединяющий вершину треугольника с серединой ее противоположной стороны.
Теоремы:
- Медиана, проведенная из вершины треугольника, делит его на два равновеликих:
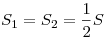 (рис. 8). (рис. 8).
- Медианы пересекаются в одной точке, называемой центроидом треугольника, и точкой пересечения делятся в отношении 2:1 считая
от вершины (рис. 9).
- Отрезки медиан, соединяющие вершины с центроидом, делят треугольник на
три равновеликих:
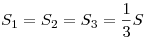 (рис. 10). (рис. 10).
- Пересекаясь, медианы делят треугольник на шесть равновеликих:
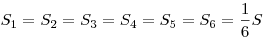 (рис. 11). (рис. 11).
- Длина медианы, проведенной к стороне c равна:
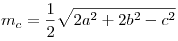 (рис. 12). (рис. 12).
Биссектриса треугольника
Биссектрисой угла называется прямая, делящая угол на две равные
части.
Биссектрисой угла треугольника называется наибольший отрезок
биссектрисы угла, лежащий внутри треугольника.
Теоремы:
- Биссектриса — множество точек, равноудаленных от сторон угла.
- Биссектриса делит сторону, к которой она проведена на отрезки, пропорциональные боковым сторонам:
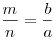 (рис. 13). (рис. 13).
Примечание. В обозначениях на рисунке имеем: 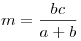 , , 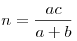 . .
- Точкой пересечения биссектрисы делятся в отношении суммы сторон
треугольника, образующих угол, в котором проведена биссектриса, к
третьей стороне:
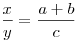 (рис. 13). (рис. 13).
- Длина биссектрисы, делящей угол
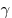 пополам, равна
удвоенному произведению сторон, деленному на их сумму и умноженному на
косинус половины угла между ними: пополам, равна
удвоенному произведению сторон, деленному на их сумму и умноженному на
косинус половины угла между ними: 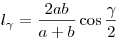 (рис. 13). (рис. 13).
- Длина биссектрисы равна:
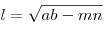 (рис. 13). (рис. 13).
- Длина биссектрисы внешнего угла треугольника равна:
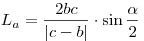 , при , при 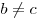 (рис. 14). (рис. 14).
- Биссектрисы треугольника пересекаются в одной точке, являющейся
центром вписанной в треугольник окружности. Радиус вписанной окружности
может быть найден по формулам:
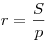 , , 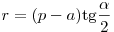 . .
Равносторонний треугольник
Равносторонний треугольник — треугольник, у которого все стороны равны: 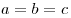 . .
Теоремы:
- Все углы равностороннего треугольника равны и равны
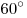 : : 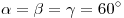 . .
- Медианы, биссектрисы и высоты равностороннего треугольника совпадают и
равны
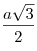 : : 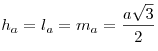 . .
- Радиус описанной вокруг равностороннего треугольника окружности:
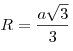 . .
- Радиус вписанной в равносторонний треугольник окружности:
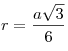 . .
- Площадь равностороннего треугольника:
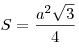 . .
Равнобедренный треугольник и его свойства
Равнобедренный треугольник — треугольник, у которого две
стороны равны (рис. 15). Эти равные стороны называются боковыми сторонами, а третья сторона — основанием треугольника.
Теоремы:
- Углы при основании равны:
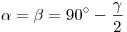 . .
- Медиана, проведенная к основанию, является биссектрисой и высотой:
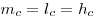 . .
- Площадь равнобедренного треугольника:
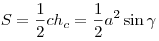 . .
Прямоугольный треугольник и его свойства
Теорема Пифагора: 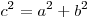 . .
Решение прямоугольного треугольника:
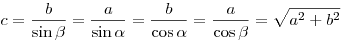 ; ;
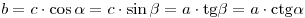 ; ;
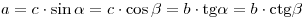 . .
Теоремы:
- Высота в прямоугольном треугольнике, проведенная из вершины прямого
угла, делит его на два подобных и подобных исходному треугольнику. Для
любых сходственных элементов (медиана, биссектриса, радиусы вписанной и
описанной окружностей и т. п.) исходного и полученных треугольников
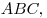 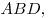 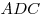 справедливо соотношение справедливо соотношение 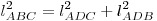 (рис. 17). (рис. 17).
- Высота, проведенная из вершины прямого угла, делит гипотенузу на
отрезки:
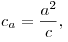 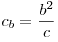 (рис. 16). Эти отрезки являются проекциями катетов на
гипотенузу. (рис. 16). Эти отрезки являются проекциями катетов на
гипотенузу.
- Высота, проведенная из вершины прямого угла, равна среднему
геометрическому проекций катетов на гипотенузу:
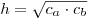 (рис. 16). (рис. 16).
- Длина высоты, проведенной из вершины прямого угла, равна отношению
произведения длин катетов и гипотенузы:
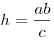 . .
- Медиана, проведенная из вершины прямого угла, равна половине
гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности (рис. 18). Радиус описанной окружности равен этой медиане и равен половине гипотенузы:
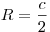 . .
- Радиус вписанной окружности равен половине суммы катетов, уменьшенной
на гипотенузы:
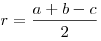 . .
- Площадь прямоугольного треугольника равна половине произведения
катетов:
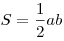 или вычисляется по любой из
следующих формул: или вычисляется по любой из
следующих формул: 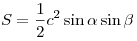 , , 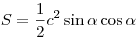 , , 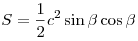 , , 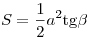 , , 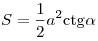 , , 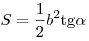 , , 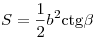 . .
Теоремы о площади треугольника
- Площадь треугольника равна:
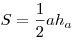 . .
- Площадь треугольника равна:
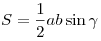 . .
- Формула Герона:
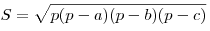 . .
- Площадь треугольника равна:
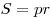 . .
- Площадь треугольника равна:
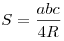 . .
- Площадь треугольника равна:
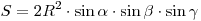 . .
- Площадь треугольника равна:
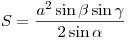 . .
- Площадь треугольника равна:
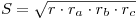 , где , где 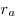 , , 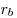 , , 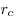 — радиусы вневписанных окружностей. — радиусы вневписанных окружностей.
- Если в треугольнике одну из сторон изменить в
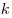 раз, а
другую в раз, а
другую в  раз, оставив без изменения угол между ними, то
площадь получившегося треугольника измениться в раз, оставив без изменения угол между ними, то
площадь получившегося треугольника измениться в 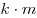 раз.
раз.
- Отношение площадей двух треугольников, у которых одна вершина
 общая, а другие вершины расположены на двух прямых,
проходящих через общая, а другие вершины расположены на двух прямых,
проходящих через  , равно отношению произведений двух сторон
каждого треугольника, содержащих вершину , равно отношению произведений двух сторон
каждого треугольника, содержащих вершину  . .
Теоремы об отрезках в треугольнике
Теорема Чевы. Пусть на сторонах треугольника  выбраны точки, [Unparseable or potentially dangerous latex formula. Error 3 ], [Unparseable or potentially dangerous latex formula. Error 3 ], выбраны точки, [Unparseable or potentially dangerous latex formula. Error 3 ], [Unparseable or potentially dangerous latex formula. Error 3 ], 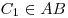 (рис. 19). Тогда отрезки [Unparseable or potentially dangerous latex formula. Error 3 ] пресекаются в одной точке тогда и только тогда, когда выполняется равенство: [Unparseable or potentially dangerous latex formula. Error 3 ]. (рис. 19). Тогда отрезки [Unparseable or potentially dangerous latex formula. Error 3 ] пресекаются в одной точке тогда и только тогда, когда выполняется равенство: [Unparseable or potentially dangerous latex formula. Error 3 ].
Обобщенная теорема Чевы. Пусть прямые 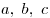 проходят через вершины проходят через вершины 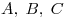 треугольника треугольника  и пересекают прямые и пересекают прямые 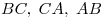 в точках [Unparseable or potentially dangerous latex formula. Error 3 ] соответственно. Тогда прямые в точках [Unparseable or potentially dangerous latex formula. Error 3 ] соответственно. Тогда прямые 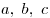 пересекаются в одной точке или параллельны тогда и только тогда, когда имеет место
равенство: [Unparseable or potentially dangerous latex formula. Error 3 ] (рис. 20). пересекаются в одной точке или параллельны тогда и только тогда, когда имеет место
равенство: [Unparseable or potentially dangerous latex formula. Error 3 ] (рис. 20).
Теорема Менелая. Пусть дан треугольник  и точки [Unparseable or potentially dangerous latex formula. Error 3 ] принадлежат соответственно прямым и точки [Unparseable or potentially dangerous latex formula. Error 3 ] принадлежат соответственно прямым 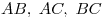 (рис. 21). Точки [Unparseable or potentially dangerous latex formula. Error 3 ] лежат на одной прямой тогда и только тогда, когда выполняется равенство: [Unparseable or potentially dangerous latex formula. Error 3 ]. (рис. 21). Точки [Unparseable or potentially dangerous latex formula. Error 3 ] лежат на одной прямой тогда и только тогда, когда выполняется равенство: [Unparseable or potentially dangerous latex formula. Error 3 ].
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
